Ressort pendu
Partie
Question
Ressort pendu (*)
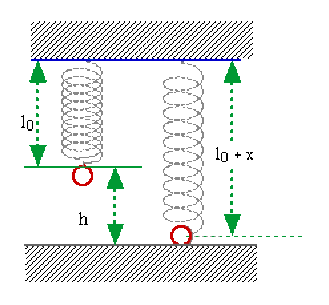
On accroche une masse de \(1 \textrm{ kg}\) à un ressort suspendu de constante de raideur\( k=50\textrm{ SI}\), on soulève la masse par un moyen extérieur au système jusqu'à ce que le ressort soit complètement détendu, et on libère brutalement l'ensemble.
Préciser la dimension de \(k\) et exprimer l'unité \(SI\) correspondante en fonction des unités fondamentales de ce système.
Calculer la vitesse de la masse au moment où elle entre en contact avec la table située \(25 \textrm{ cm}\) au-dessous du point de départ.
Aide simple
Utiliser la conservation de l'énergie mécanique
Solution détaillée
La relation de définition de \(k\) :\(\displaystyle{\overrightarrow F=-kx\overrightarrow i}\) où \(x\) est l'allongement du ressort montre que la dimension de \(k\) s'écrit : \([k] = M T^{-2}\) et s'exprime donc en \(Nm^{-1}\).
Avant qu'on lâche la masse l'énergie mécanique du système, en prenant pour référence de l'énergie potentielle la surface de la table prise pour altitude \(0\) (\(W_p = 0\) à la surface), \(x\) étant la compression du ressort est :
\(W_0= \frac{1}{2}k{x_0}^2+\frac{1}{2}m{v_0}^2+mgh=0+0+mgh\)
Au moment du contact avec la table
\(\displaystyle{W_{\textrm{final}}=\frac{1}{2}kx_f^2+\frac{1}{2}mv_f^2+0\textrm{ où }x_f=h}\)
De la conservation de l'énergie mécanique nous tirons :
\(\displaystyle{mgh=\frac{1}{2}kx_f^2+\frac{1}{2}mv_f^2}\)
où
\(\displaystyle{v_f=\sqrt{2gh-\frac{kx_f^2}{m}}}\)
A.N. : \(v_f = 1,33 \textrm{ ms}^{-1}\)