Equation de conjugaison
Partie
Question
Soit un dioptre sphérique \((D)\) de sommet \(S\), de centre \(C\) et de foyer image \(F'\). Le stigmatisme est supposé réalisé.
A l'aide de l'équation fondamentale du dioptre sphérique, formuler :
la distance focale image \(f '\) d'un dioptre sphérique en fonction de son rayon de courbure \(R=\overline{SC}=- 10 cm\) et des indices des milieux d'entrée et de sortie \(n_1=1,5\) et \(n_2=1\). Calculer \(f'\) avec ces valeurs.
la distance focale objet \(f\) avec les mêmes paramètres.
Aide simple
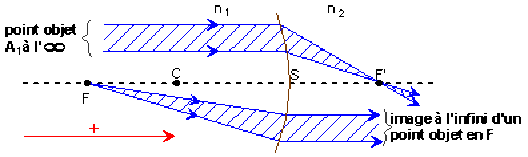
Le foyer image d'un dioptre sphérique est l'image d'un point de l'axe infiniment éloigné.
La distance focale image d'un dioptre sphérique est la mesure algébrique du segment \(\overline{SF'}\) séparant le sommet \(S\) du dioptre du foyer image \(F'\).
Le foyer objet d'un dioptre sphérique est le point de l'axe dont l'image est rejetée à l'infini sur l'axe.
La distance focale objet d'un dioptre sphérique est la mesure algébrique du segment \(\overline{SF}\) qui séparent le sommet \(S\) du dioptre, du foyer objet \(F\).
Aide détaillée
Les conditions de stigmatisme sont réalisées, les foyers existent donc et peuvent être déterminés à l'aide de l'équation fondamentale du dioptre sphérique, avec origine des coordonnées au sommet \(S\) du dioptre.
\(\frac{n_{2}}{\overline{SA_{2}}}-\frac{n_{1}}{\overline{SA_{1}}}=\frac{n_{2}-n_{1}}{\overline{SC}}\)

Rappel de cours
Le dioptre sphérique n'est rigoureusement stigmatique que pour les points de sa surface et son centre
Il y a stigmatisme approché pour tout point de l'espace qui n'envoie sur le dioptre sphérique qu'un pinceau lumineux dont le rayon moyen lui est normal, c'est à dire peu incliné par rapport à l'axe du dioptre ou encore formé de rayons paraxiaux.
Tout rayon incident parallèle à l'axe optique se réfracte en passant par le foyer image F'.
Un rayon incident passant par le foyer objet du dioptre se réfractera en un rayon parallèle à l'axe optique du dioptre.
Pour construire l'image d'un objet plan :
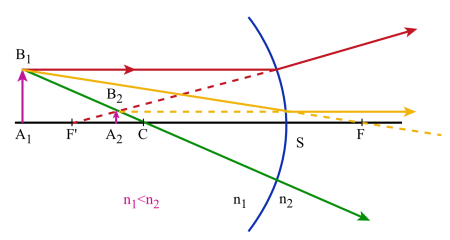
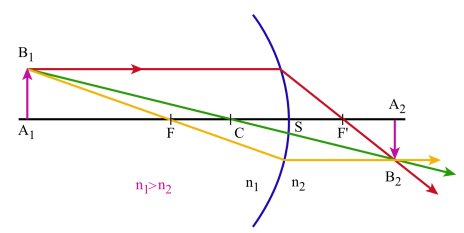
on utilise 3 rayons particuliers :
un rayon passant par le centre du dioptre et qui n'est pas dévié à la traversée de celui-ci
un rayon issu de \(B_1\) et passant par le foyer objet \(F\) : il est réfracté suivant une parallèle à l'axe principal
un rayon issu de \(B_1\) et parallèle à l'axe principal : il est réfracté suivant un rayon qui passe par le foyer image \(F'\).
Formules de conjugaison :
Origine au sommet
\(\frac{n_1}{\overline{SA_1}}.\frac{n_2}{\overline{SA_2}}=\frac{n_1-n_2}{\overline{SC}}\)
\(\gamma=\frac{n_1}{n_2}\frac{\overline{SA_2}}{\overline{SA_1}}\)
Origine au centre
\(\frac{n_1}{\overline{CA_2}}.\frac{n_2}{\overline{CA_1}}=\frac{n_1-n_2}{\overline{CS}}\)
\(\gamma=\frac{\overline{A_2B_2}}{\overline{A_1B_1}}=\frac{\overline{CA_2}}{\overline{CA_1}}\)
Origine aux foyers
\(\overline{FA_1}\overline{F'A_2}=\overline{SF}\overline{SF'}=ff'\)
\(\gamma=-\frac f{\overline{FA_1}}=\frac{\overline{F'A_1}}{f'}\)
Relation de Lagrange-Helmholtz :
Solution détaillée
\(\frac{n_2}{\overline{SA_2}}-\frac{n_1}{\overline{SA_1}}=\frac{n_2-n_1}{\overline{SC}}\) (1) \(\overline{SA_1}\rightarrow\pm\infty\Rightarrow\overline{SA_2}\rightarrow\overline{SF'}=f'\)
soit \(\overline{SF'}=f'=\frac{n_2}{n_2-n_1}\) (2) \(\overline{SF'}=f'=\left(\frac1{1-1,5}\right)\times(-10 \textrm{cm})=20 \textrm{cm}\)
Si \(\overline{SA_2}\rightarrow\pm\infty\Rightarrow\overline{SA_1}\rightarrow\overline{SF}=f\)
soit \(\overline{SF}=f=\frac{n_1}{n_1-n_2}.\overline{SC}\) (3) \(\overline{SF}=f=\left(\frac{1,5}{1,5-1}\right)\times(-10\textrm{cm})=-30\textrm{cm}\)