Grandissement transversal
Partie
Question
Soient \(B_1\), \(B_2\) deux points conjugués par un dioptre sphérique du centre \(C\) et de sommet \(S\). Dans l'approximation de GAUSS :
Vérifier géométriquement les relations de grandissement algébrique transversal \(\gamma=-f/\overline{FA_1}=-\overline{F'A_2}/f'\).
En déduire la relation de conjugaison, avec origine aux foyers \(F\) et \(F'\). \(\overline{FA_{1}} . \overline{F'A_{2}} = ff'\) que l'on pourra écrire \(x_0.x_i = f.f'\)
Utiliser la relation de Thalès
Aide simple
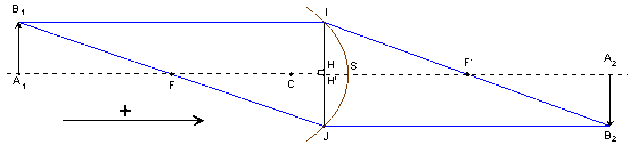
Dans l'approximation de Gauss les projections \(H'\) de \(I\) et \(H\) de \(J\) sont pratiquement confondues avec \(S\).
\(\gamma=\frac{\overline{A_2B_2}}{\overline{A_1B_1}}=\frac{\overline{A_2B_2}}{\overline{H'I}}\quad\gamma=\frac{\overline{A_2B_2}}{\overline{A_1B_1}}=\frac{\overline{HJ}}{\overline{A_1B_1}}\)
La relation de Thalès dans les paires de triangles semblables \(FA_1B_1\), \(FHJ\) puis \(F'A_2B_2\) et \(F'HI\) donnent les relations :
\(\gamma=\frac{\overline{A_2B_2}}{\overline{H'I}}=\frac{\overline{F'A_2}}{\overline{F'H'}}\)(3)
\(\gamma=\frac{\overline{HJ}}{\overline{A_1B_1}}=\frac{\overline{FH}}{\overline{FA_1}}\)(4)
Rappel de cours
Le dioptre sphérique n'est rigoureusement stigmatique que pour les points de sa surface et son centre
Il y a stigmatisme approché pour tout point de l'espace qui n'envoie sur le dioptre sphérique qu'un pinceau lumineux dont le rayon moyen lui est normal, c'est à dire peu incliné par rapport à l'axe du dioptre ou encore formé de rayons paraxiaux.
Tout rayon incident parallèle à l'axe optique se réfracte en passant par le foyer image F'.
Un rayon incident passant par le foyer objet du dioptre se réfractera en un rayon parallèle à l'axe optique du dioptre.
Pour construire l'image d'un objet plan :
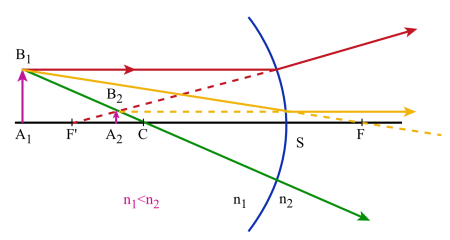
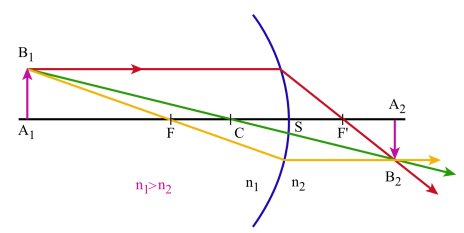
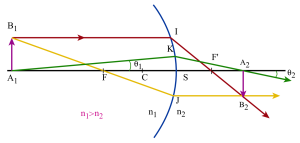
on utilise 3 rayons particuliers :
un rayon passant par le centre du dioptre et qui n'est pas dévié à la traversée de celui-ci
un rayon issu de \(B_1\) et passant par le foyer objet \(F\) : il est réfracté suivant une parallèle à l'axe principal
un rayon issu de \(B_1\) et parallèle à l'axe principal : il est réfracté suivant un rayon qui passe par le foyer image \(F'\).
Formules de conjugaison :
Origine au sommet
\(\frac{n_1}{\overline{SA_1}}.\frac{n_2}{\overline{SA_2}}=\frac{n_1-n_2}{\overline{SC}}\)
\(\gamma=\frac{n_1}{n_2}\frac{\overline{SA_2}}{\overline{SA_1}}\)
Origine au centre
\(\frac{n_1}{\overline{CA_2}}.\frac{n_2}{\overline{CA_1}}=\frac{n_1-n_2}{\overline{CS}}\)
\(\gamma=\frac{\overline{A_2B_2}}{\overline{A_1B_1}}=\frac{\overline{CA_2}}{\overline{CA_1}}\)
Origine aux foyers
\(\overline{FA_1}\overline{F'A_2}=\overline{SF}\overline{SF'}=ff'\)
\(\gamma=-\frac f{\overline{FA_1}}=\frac{\overline{F'A_1}}{f'}\)
Relation de Lagrange-Helmholtz :
Solution détaillée
Dans l'approximation de GAUSS, les points \(H\) et \(H'\), projection de \(I\) et \(I'\) peuvent être confondus avec S.
(3) \(\overline{F'H'}\#\overline{F'S}=-f'\quad\gamma=-\frac{\overline{F'A_2}}{\overline{H'F'}}=-\frac{\overline{F'A_2}}{f'}\)
(4) \(\overline{FH}\#\overline{FS}=-f\quad\gamma=-\frac{\overline{HF}}{\overline{FA_1}}=-\frac f{\overline{FA_1}}\)
les relations (3) et (4) entrainent, avec \(x_0=\overline{FA_1}\) et \(x_i=\overline{F'A_2}\) que :
\(x_0\cdot x_i=\overline{FA_1}\cdot\overline{F'A_2}=ff'\)
NB : Pour d'évidentes raisons de visibilité \((H^1 H'^1 S)\), les schémas ne respectent pas les conditions de GAUSS.