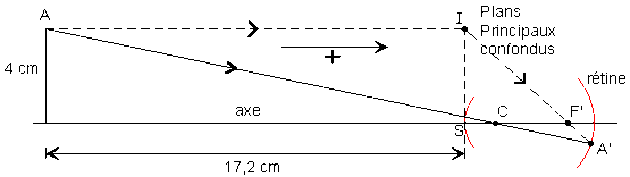
Foyer image de l'œil en accommodation maximum
Partie
Question
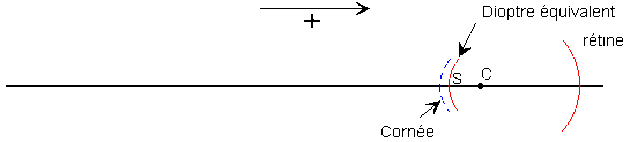
On démontre qu'un œil peut être réduit à un dioptre unique de centre \(C\), de rayon \(R~ \#~ 6~ \textrm{mm}\) de sommet \(S\) situé 2 mm en arrière de la cornée.
Déterminer géométriquement, à l'aide d'un dioptre équivalent, la position du foyer image \(F'\) de l'oeil qui accommode sur un objet situé à son proximum \(P\) sachant que la rétine est à 25 mm du sommet de la cornée et le segment cornée \(-P = - 17 \textrm{cm}\).
Tracer la marche de rayons particuliers
Aide simple
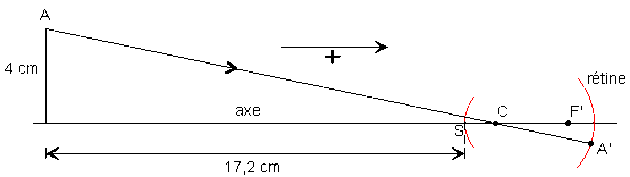
Construire, à l'aide d'une simple règle, l'image d'un point \(A\) situé à 4 cm de l'axe et à 17,2 cm du sommet du dioptre sphérique équivalent de cet œil.
Aide détaillée
Le rayon issu du point objet \(A\) et de direction \(AC\) n'est pas dévié car perpendiculaire au dioptre sphérique. Il rencontre la rétine au point image \(A'\).
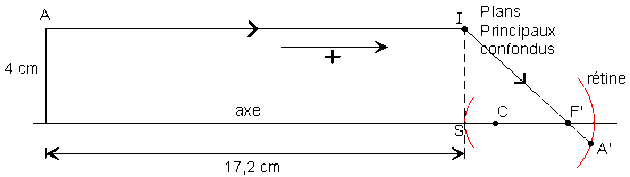
Un rayon issu du point objet \(A\) parallèle à l'axe a une trajectoire émergente définie par \(A'\) et un point \(I\) du plan principal image situé à 4 cm de l'axe. Cette trajectoire émergente contient \(F'\).
Rappel de cours
Le dioptre sphérique n'est rigoureusement stigmatique que pour les points de sa surface et son centre
Il y a stigmatisme approché pour tout point de l'espace qui n'envoie sur le dioptre sphérique qu'un pinceau lumineux dont le rayon moyen lui est normal, c'est à dire peu incliné par rapport à l'axe du dioptre ou encore formé de rayons paraxiaux.
Tout rayon incident parallèle à l'axe optique se réfracte en passant par le foyer image F'.
Un rayon incident passant par le foyer objet du dioptre se réfractera en un rayon parallèle à l'axe optique du dioptre.
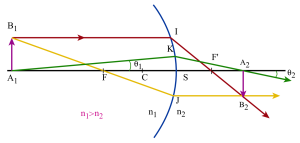
Pour construire l'image d'un objet plan :
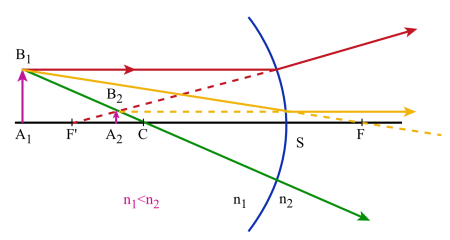
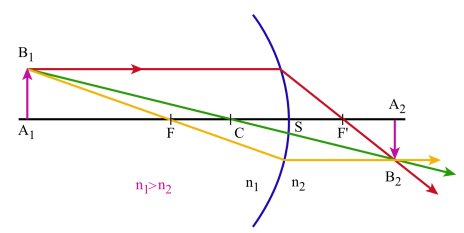
on utilise 3 rayons particuliers :
un rayon passant par le centre du dioptre et qui n'est pas dévié à la traversée de celui-ci
un rayon issu de \(B_1\) et passant par le foyer objet \(F\) : il est réfracté suivant une parallèle à l'axe principal
un rayon issu de \(B_1\) et parallèle à l'axe principal : il est réfracté suivant un rayon qui passe par le foyer image \(F'\).
Formules de conjugaison :
Origine au sommet
\(\frac{n_1}{\overline{SA_1}}.\frac{n_2}{\overline{SA_2}}=\frac{n_1-n_2}{\overline{SC}}\)
\(\gamma=\frac{n_1}{n_2}\frac{\overline{SA_2}}{\overline{SA_1}}\)
Origine au centre
\(\frac{n_1}{\overline{CA_2}}.\frac{n_2}{\overline{CA_1}}=\frac{n_1-n_2}{\overline{CS}}\)
\(\gamma=\frac{\overline{A_2B_2}}{\overline{A_1B_1}}=\frac{\overline{CA_2}}{\overline{CA_1}}\)
Origine aux foyers
\(\overline{FA_1}\overline{F'A_2}=\overline{SF}\overline{SF'}=ff'\)
\(\gamma=-\frac f{\overline{FA_1}}=\frac{\overline{F'A_1}}{f'}\)
Relation de Lagrange-Helmholtz :
Solution détaillée
Le système optique de l'œil est remplacé par un dioptre situé 24,8 mm en avant de la rétine sur laquelle converge en \(A'\) les rayons issus de \(A\). Un rayon issu de \(A\) et parallèle à l'axe rencontrerait le plan principal image en \(I\) à 4 cm de l'axe et se réfracterait selon la direction \(IA'\). Par définition, l'intersection de ce rayon émergent avec l'axe est le foyer image \(F'\) du dioptre.
NB : Un tel rayon ne peut exister, cette construction ne pourrait correspondre à une réalité qu'avec un point \(A\) à 4 mm de l'axe au plus mais la faible inclinaison de \(IA'\) qui résulterait de cette réalité entrainerait beaucoup d'imprécision sur \(F'\).
La construction proposée souligne l'intérêt de la notion de plans principaux.