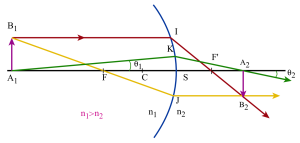
Notion de plans principaux
Partie
Question
Vérifier à l'aide d'un schéma et déterminer, à l'aide de la définition ci-dessous, les surfaces principales du dioptre sphérique.
On appelle surfaces principales (ou plans principaux) d'un système optique centré, les surfaces conjuguées lieu d'un petit objet \(A_1B_1\) d'image \(A_2B_2\) dans ce système, pour lesquels le grandissement linéaire transversal vaut : \(\gamma=\frac{A_2B_2}{A_1B_1}=+1\).
Considérer la surface du dioptre sphérique
Aide simple
Vérifier géométriquement que tout point de la surface du dioptre est sa propre image ; que vaut alors le grandissement d'un petit segment \(A_1B_1\) collé à la surface ?
Rappel de cours
Le dioptre sphérique n'est rigoureusement stigmatique que pour les points de sa surface et son centre
Il y a stigmatisme approché pour tout point de l'espace qui n'envoie sur le dioptre sphérique qu'un pinceau lumineux dont le rayon moyen lui est normal, c'est à dire peu incliné par rapport à l'axe du dioptre ou encore formé de rayons paraxiaux.
Tout rayon incident parallèle à l'axe optique se réfracte en passant par le foyer image F'.
Un rayon incident passant par le foyer objet du dioptre se réfractera en un rayon parallèle à l'axe optique du dioptre.
Pour construire l'image d'un objet plan :
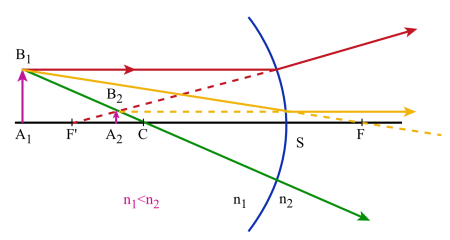
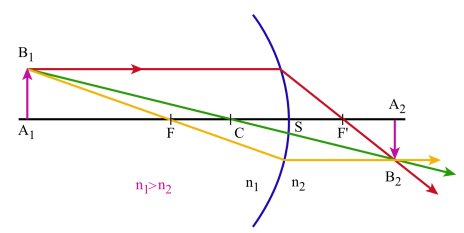
on utilise 3 rayons particuliers :
un rayon passant par le centre du dioptre et qui n'est pas dévié à la traversée de celui-ci
un rayon issu de \(B_1\) et passant par le foyer objet \(F\) : il est réfracté suivant une parallèle à l'axe principal
un rayon issu de \(B_1\) et parallèle à l'axe principal : il est réfracté suivant un rayon qui passe par le foyer image \(F'\).
Formules de conjugaison :
Origine au sommet
\(\frac{n_1}{\overline{SA_1}}.\frac{n_2}{\overline{SA_2}}=\frac{n_1-n_2}{\overline{SC}}\)
\(\gamma=\frac{n_1}{n_2}\frac{\overline{SA_2}}{\overline{SA_1}}\)
Origine au centre
\(\frac{n_1}{\overline{CA_2}}.\frac{n_2}{\overline{CA_1}}=\frac{n_1-n_2}{\overline{CS}}\)
\(\gamma=\frac{\overline{A_2B_2}}{\overline{A_1B_1}}=\frac{\overline{CA_2}}{\overline{CA_1}}\)
Origine aux foyers
\(\overline{FA_1}\overline{F'A_2}=\overline{SF}\overline{SF'}=ff'\)
\(\gamma=-\frac f{\overline{FA_1}}=\frac{\overline{F'A_1}}{f'}\)
Relation de Lagrange-Helmholtz :
Solution détaillée
Tout point objet de la surface du dioptre est sa propre image. Un bipoint objet \(A_1B_1\) de la surface du dioptre a une image \(A_2B_2\) qui lui est identique \(\overline{A_2B_2}=\overline{A_1B_1}\) et \(\gamma=\overline{A_2B_2}/\overline{A_1B_1}=+1\).
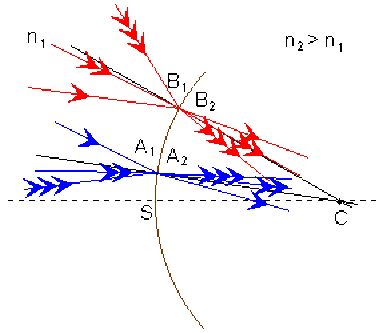
La surface du dioptre est une surface double (elle est à la fois objet et image) pour laquelle \(\gamma=+1\).
Si l'on fait abstraction de la courbure du dioptre sphérique, ces surfaces principales peuvent être appelées plans principaux.