Calcul d'une intensité
Partie
Question
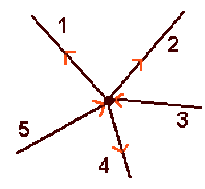
Donner le sens et la valeur de l'intensité manquante :
\(a)\; I_1 = 1 \textrm{ A} ; I_2 = 2 \textrm{ A} ; I_3 = ? \textrm{ A} ; I_4 = 5 \textrm{ A} ; I_5 = 3 \textrm{ A}\)
\(b)\; I_1 = ? \textrm{ A} ; I_2 = 4 \textrm{ A} ; I_3 = 9 \textrm{ A} ; I_4 = 8 \textrm{ A} ; I_5 = 2 \textrm{ A}\)
\(c)\; I_1 = 7 \textrm{ A} ; I_2 = ? \textrm{ A} ; I_3 = 5 \textrm{ A} ; I_4 = 3 \textrm{ A} ; I_5 = 6 \textrm{ A}\)
Aide simple
Appliquer la loi des nœuds.
Aide détaillée
A un noeud d'un réseau, la somme des intensités des courants qui arrivent est égale à la somme des intensités qui repartent.
Solution simple
\(a)\; I_3 = 5 \textrm{ A}\)
\(b)\; I_1 = -1 \textrm{ A}\)
\(c)\; I_2 = 1 \textrm{ A}\)
Solution détaillée
A un nœud d'un réseau, la somme des intensités des courants qui arrivent est égale à la somme des intensités qui repartent ; donc :
\(I_3 + I_5 = I_1 + I_2 + I_4\)
a) \(I_3 = I_1 + I_2 + I_4 - I_5 = 1 +2 + 5 - 3 = 5 \textrm{ A}\)
b) \(I_1 = I_3 + I_5 - I_2 - I_4 = 9 + 2 - 4 - 8 = -1 \textrm{ A}\) le courant circule donc dans l'autre sens, c'est à dire vers le nœud.
c) \(I_2 = I_3 + I_5 - (I_1 + I_4) = 5 + 6 - (7 + 3) = 1 \textrm{ A}\)