Détermination d'un courant
Partie
Question
Calculer l'intensité débitée par chaque générateur dans la branche CD ; en déduire le sens et l'intensité du courant dans cette branche quand le réseau est complet.

\(\displaystyle{E_1 = 12 \textrm{ V} ; E_2 = 6 \textrm{ V} ; R_1 = 10 \;\Omega ; R_2 = 20 \;\Omega ; R_3 = 15 \Omega ; R_4 = 10 \Omega ; R_5 = 50 \;\Omega ; R_6 = 2 \;\Omega}\)
Aide simple
Penser à remplacer successivement chaque f.é.m. par un court-circuit.
Aide détaillée
Pour calculer le courant débité par chaque générateur dans la branche \(CD\), on peut remplacer le réseau par un réseau équivalent plus simple, à condition de conserver la branche \(CD\) dans le nouveau réseau.
Solution simple
Courant débité par le générateur \(E_1 \textrm{ dans }R_5 : I = 7 \textrm{ mA} (\textrm{ de D vers A })\)
Courant débité par le générateur \(E_2 \textrm{ dans }R_5 : I = 105 \textrm{ mA (de D vers A) }\)
Courant total dans \(R_5 : I_5 = 112 \textrm{ mA ( de D vers A) }\)
Solution détaillée
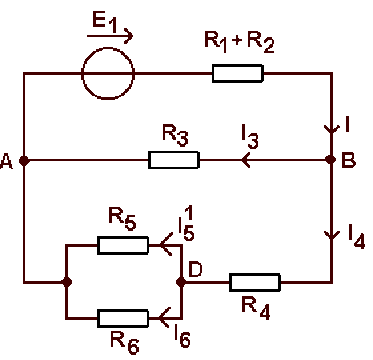
On applique le théorème de superposition :
Courant débité par\( E_1\) seul dans \(R_5\) :
quand on enlève \(E_2\), et compte tenu du fait que \(A \textrm{ et }C\) sont un même nœud, le réseau devient :
Le courant I débité par le générateur se divise en \(I_3 \textrm{ et } I_4\), qui se divise à son tour en \(I_5 \textrm{ et }I_6\).
Soit \(R_{AB}\) la résistance équivalente à l'ensemble \(R_3 \textrm{ et }R_6\), vu de \(A \textrm{ et }B\) ; d'après les lois d'association des conducteurs ohmiques :
\(\displaystyle{R_{AB}=\frac{1}{\frac{1}{R_3}+\frac{1}{R_4+\frac{1}{\frac{1}{R_5}+\frac{1}{R_6}}}}=6,64\;\Omega}\)
L'intensité I vaut donc :
\(\displaystyle{I=\frac{E}{R_1+R_2+R_{AB}}=0,327\textrm{ A}}\)
d'où :
\(\displaystyle{I_4=I.\frac{G_{456}}{G_3+G_{456}}=I.\frac{R_3}{R_3+R_4+\frac{1}{\frac{1}{R_5}+\frac{1}{R_6}}}=0,182\textrm{ A}}\)
et \(\displaystyle{I_5^1=I_4.\frac{G_5}{G_5+G_6}=I_4.\frac{R_6}{R_5+R_6}=7\textrm{ mA}}\) de \(D\) vers \(A\)
2)Courant débité par \(E_2\) seul
Quand on remplace \(E_1\) par un court-circuit, et compte tenu du fait que \(A \textrm{ et }C\) forment un seul nœud, le circuit devient :
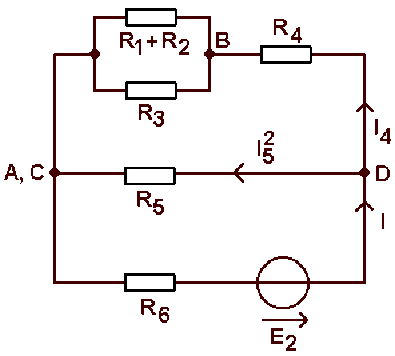
Le courant I débité par \(E_2\) se divise en\( I_4\) et \(I_5^2\)
Soit \(R_{AD}\) la résistance équivalente à l'ensemble des dipôles \(R_1 \textrm{ à }R_5, \textrm{ vu de A et D }\)
\(\displaystyle{R_{AD}=\frac{1}{\frac{1}{R_5}+\frac{1}{R_4+\frac{1}{\frac{1}{R_1+R_2}+\frac{1}{R_3}}}}}\)
d'où : \(\displaystyle{I=\frac{E_2}{R_6+R_{AD}}=368,4\textrm{ mA}}\)
et \(\displaystyle{I_5^2=I.\frac{G_5}{G_{AD}}=I.\frac{R_{AD}}{R_5}=105\textrm{ mA}}\) circulant de D vers A.
3) Pour l'ensemble des deux générateurs, le courant circule donc de \(D \textrm{ vers }A\) et a pour intensité :
\(\displaystyle{I_5=I_5^1+I_5^2}\)
\(I_5 = 105 + 7,0 = 112 \textrm{ mA}\)