Générateur de Thévenin (1)
Partie
Question
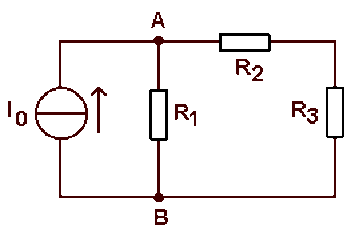
Déterminer les caractéristiques du générateur de Thevenin équivalent à ce réseau, vu de \(A \textrm{ et }B\) :
Application numérique : \(I_0 = 100 \mu \textrm{A}; R_1 = 100 \;\Omega ; R_2 = 470 \;\Omega ; R_3 = 330 \;\Omega\)
Aide simple
La f.é.m. de Thévenin est la tension à vide entre \(A \textrm{ et }B\).
La résistance interne est la résistance du réseau passif vu de\( A \textrm{ et }B\).
Aide détaillée
Calculer \(R_{AB} ; E = R_{AB}.I_0 ; r = R_{AB}\)
Solution simple
\(E = 8,89 \textrm{ mV}\)
\(r = 88,9\;\Omega\)
Solution détaillée
A vide, le générateur débite un courant d'intensité \(I_0\) qui se répartit entre les deux branches \(R_1 \textrm{ et }(R_2, R_3) \textrm{ de bornes A et B}\). Soit \(R_{AB}\) la résistance équivalente :
\(\displaystyle{R_{AB}=\frac{1}{\frac{1}{R_1}+\frac{1}{R_2+R_3}}=88,9\;\Omega}\)
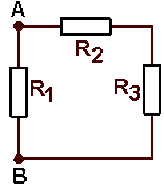
Le réseau est donc équivalent à :
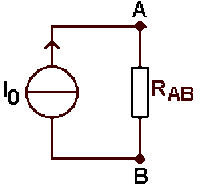
La f.é.m. de Thévenin est la tension à vide entre \(A\textrm{ et }B\).
D'où \(E = R_{AB}.I_0 = 8,89 \textrm{ mV}\)
La résistance interne est la résistance du réseau vu de \(A \textrm{ et }B : r = R_{AB}\)
Le modèle de Thévenin équivalent au réseau vu de \(A \textrm{ et }B\) est finalement :
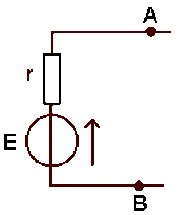
avec \(E = 8,89\textrm{ mV}, r = 88,9\;\Omega\)