Générateur de Thévenin (3)
Partie
Question
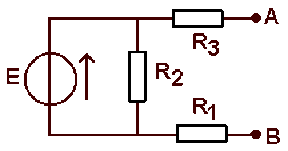
Déterminer les caractéristiques du générateur de Thévenin équivalent à ce réseau vu de \(A\textrm{ et }B\) :
Application numérique : \(E = 30 \textrm{ V} ; R_1 = 100 \;\Omega ; R_2 = 470 \;\Omega ; R_3 = 330 \;\Omega\)
Aide simple
La f.é.m. de Thévenin est la tension à vide entre \(A \textrm{ et }B\).
La résistance interne est la résistance du réseau passif vu de \(A \textrm{ et }B\).
Aide détaillée
A vide, il n'y a pas de courant à travers \(R_1 \textrm{ et }R_3\).
Solution simple
\(E' = 30 \textrm{ V}\)
\(r' = 900\;\Omega\)
Solution détaillée
A vide, il n'y a pas de courant à travers \(R_1 \textrm{ et }R_3\), donc la f.é.m. \(E'\) est égale à la tension aux bornes de \(R_2\), qui vaut \(E = 30 \textrm{ V}\).
La résistance du générateur est la résistance du réseau vu de \(A \textrm{ et }B\) ; en remplaçant\( E\) par un court-circuit, on obtient le schéma suivant :
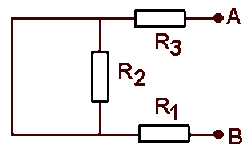
équivalent à :
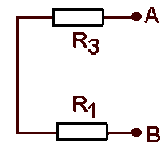
puisqu'un court-circuit en parallèle sur une résistance est équivalent au court-circuit seul, quelle que soit la résistance. Finalement :
\(r = R_{AB} = R_1 + R_3 = 430\;\Omega\)
D'où le schéma de Thévenin équivalent au réseau vu de \(A \textrm{ et }B\)
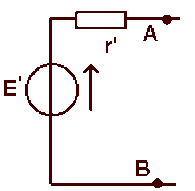
avec \(E' = 30\textrm{ V et }r' = 430 \;\Omega\)