Analyse d'un réseau par différentes méthodes
Partie
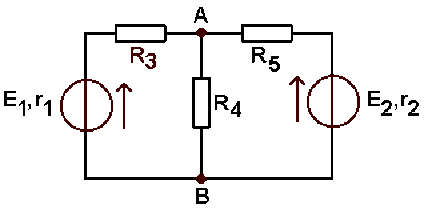
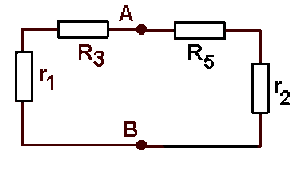
Dans le réseau ci-contre :
\(E_1 = 8 \textrm{ V}\) ;
\(r_1 = 2\;\Omega\) ;
\(E_2 = 15 \textrm{ V}\) ;
\(r_2 = 5 \;\Omega\) ;
\(R_3 = 8 \;\Omega\) ;
\(R_4 = 10\;\Omega\)
\(R_5 = 15\;\Omega\)
Calculer l'intensité \(I_4\) du courant qui traverse la branche de résistance \(R_4\).
Question
Méthode : Lois de Kirchoff
Aide simple
Ne pas choisir pour squelette la branche contenant \(R_4\)
Solution simple
\(I_4 = 0,62 \textrm{ A} (\textrm{ de A vers B})\)
Solution détaillée
Méthode : Lois de Kirchoff
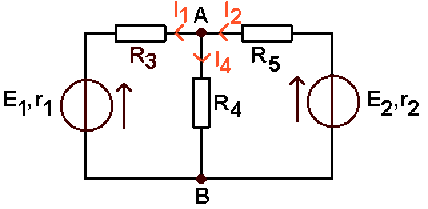
Il faut prendre pour squelette la branche de droite ou celle de gauche ; si on prend celle de gauche, les inconnues sont \(I_2\), courant débité par \(E_2\textrm{ et }I_4\), courant traversant \(R_4\).
L'intensité \(I_1\) dans le squelette est donnée par la loi des noeuds : \(I_1 = I_2 - I_4\)
Les sens indiqués sur la figure prennent en compte la relation numérique \(E_2 > E_1\).
La maille de gauche et la maille de droite sont indépendantes ; d'après la loi des mailles :
\(\displaystyle{R_4.I_4-(R_3+r_1).(I_2-I_4)-E_1=0}\)
\(\displaystyle{E_2-(r_2+R_5).I_2-R_4.I_4=0}\)
On obtient un système de 2 équations linéaires à 2 inconnues :
\(\displaystyle{(R_4+R_3+r_1).I_4-(R_3+r_1).I_2=E_1\quad(1)}\)
\(\displaystyle{R_4.I_4+(r_2+R_5).I_2=E_2\quad(2)}\)
que l'on résout par la méthode de substitution :
\(\displaystyle{(2)\quad I_2=\frac{E_2-R_4.I_4}{r_2+R_5}}\) à reporter dans (1)
Ou la méthode de Kramer :
\(\displaystyle{\begin{array}{lll}I_4&=&\frac{\left|\begin{array}{ccc}E_1&-(R_3+r_1)\\E_2&r_2+R_5\end{array}\right|}{\left|\begin{array}{ccc}R_4+R_3+r_1&-(R_3+r_1)\\R_4&r_2+R_5\end{array}\right|}\\\\&=&\frac{(r_2+R_5).E_1+(R_3+r_1).E_2}{(r_2+R_5)(r_1+R_3+R_4)+R_4.(r_1+R_3)}=0,62\textrm{ A}\end{array}}\)
Question
Méthode :Théorème de superposition
Aide simple
Méthode : Théorème de superposition
Remplacer successivement chaque générateur par sa résistance interne.
Rappel de cours
voir la page Théorème de superposition
Solution simple
\(\displaystyle{I_4 = 0,62 \textrm{ A (de A vers B)}}\)
Solution détaillée
Méthode : Théorème de superposition
Courant débité par \(E_1\) dans \(R_4\) :
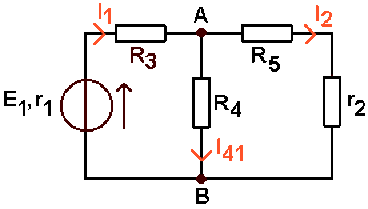
On remplace le générateur {\(E_2, r_2\)} par \(r_2\). Le générateur {\(E_1, r_1\)} débite à travers \(R_3\) un courant d'intensité \(I_1\) qui se divise en\( I_{41}\) à travers \(R_4 \textrm{ et }I_2\) à travers \(R_5 \textrm{ et }r_2\).
L'ensemble \(R_4, R_5, r_2\) vu de \(A \textrm{ et }B\) a pour résistance équivalente :
\(\displaystyle{R_{AB}=\frac{1}{\frac{1}{R_4}+\frac{1}{r_2+R_5}}=\frac{20}{3}\;\Omega}\)
d'où \(\displaystyle{I_1=\frac{E_1}{r_1+R_3+R_{AB}}=0,48\textrm{ A}}\)
et \(\displaystyle{I_{41}=I_1.\frac{G_4}{G_{AB}}=0,32\textrm{ A}}\)
Courant débité par\( E_2\) dans \(R_4\) :
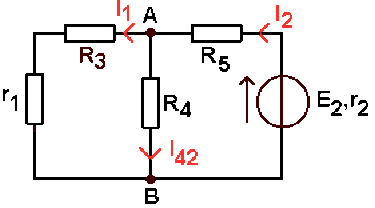
On remplace le générateur {\(E_1, r_1\)} par \(r_1\). Le générateur {\(E_2, r_2\)} débite à travers \(R_5\) un courant d'intensité \(I_2\) qui se divise en \(I_{42}\) à travers \(R_4 \textrm{ et }I_1\) à travers \(R_3 \textrm{ et }r_1\).
L'ensemble \(r_1, R_3, R_4 \textrm{ vu de A et B }\) a pour résistance équivalente :
\(\displaystyle{R_{AB}=\frac{1}{\frac{1}{R_4}+\frac{1}{r_1+R_3}}=5\;\Omega}\)
d'où \(\displaystyle{I_2=\frac{E_2}{r_2+R_5+R_{AB}}=0,6\textrm{ A}}\)
et \(\displaystyle{I_{42}=I_2.\frac{G_4}{G_{AB}}=0,3\textrm{ A}}\)
Pour l'ensemble des deux générateurs , le courant à travers \(R_4\) est donc :
\(\displaystyle{I_4=I_{41}+I_{42}}=0,62\textrm{ A de A vers B}\)
Question
Méthode :Courant de maille de Maxwell
Aide simple
Méthode : Courant de maille de Maxwell
Choisir les mailles de façon à ce que \(R_4\) soit traversé par un seul courant de maille.
Rappel de cours
Voir la page Méthode des courants de maille
Solution simple
\(I_4 = 0,62 \textrm{ A (de A vers B)}\)
Solution détaillée
Méthode : Courants de maille de Maxwell
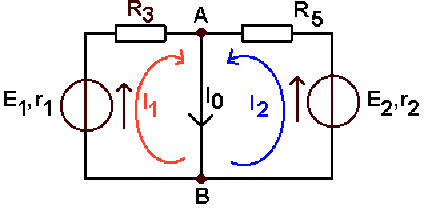
Il y a deux noeuds et trois branches, donc deux mailles indépendantes. On peut donc choisir indifféremment deux des trois mailles possibles (gauche, droite, extérieure). Pour que \(R_4\) soit traversée par un seul courant de maille, on peut choisir, par exemple, la maille de droite et la maille extérieure.
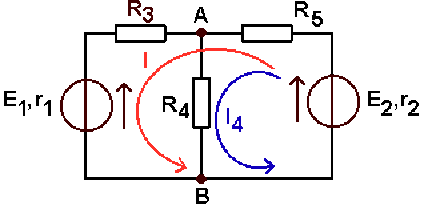
Soit I l'intensité du courant dans la maille extérieure
Ecrivons les équations aux mailles :
Maille de droite :\( E_2 - (r_2 + R_5)(I + I_4) - R_4.I_4 = 0\)
Maille extérieure : \(E_2 - (R_2 + R_5)(I + I_4) - (r_1 + R_3).I - E_1 = 0\)
En regroupant les termes, il vient :
\((r_2 + R_4 + R_5).I_4 + (r_2 + R_5).I = E_2\quad (1)\)
\((r_2 + R_5).I_4 + (r_1 + r_2 + R_3 + R_5).I = E_2 - E_1 \quad(2)\)
que l'on peut résoudre par substitution :
\(\displaystyle{I=\frac{E_2-(r_2+R_4+R_5).I_4}{r_2+R_5}}\)
à reporter dans (2), ou par la méthode de Kramer :
On peut simplifier le système d'équations en remplaçant (2) par (1) - (2) :
\(R_4.I_4 - (r_1 + R_3).I = E_1\)
\(I_4=\displaystyle{\frac{\left|\begin{array}{ccc}E_2&r_2+R_5\\E_1&-(r_1+R_3)\end{array}\right|}{\left|\begin{array}{ccc}r_2+R_4+R_5&r_2+R_5\\R_4&-r_1+R_3\end{array}\right|}}=0,62\textrm{ A}\)
Question
Méthode : Potentiels de noeud de Maxwell
Aide simple
Méthode : Potentiels de noeud de Maxwell
Poser \(V_B = 0\).
Exprimer les intensités dans les 3 branches en fonction de \(V_B - V_A\), puis appliquer la loi des noeuds.
Aide détaillée
\(I_4 = 0,62 \textrm{ A (de A vers B) }\)
Solution détaillée
Méthode : Potentiels de noeud de Maxwell

Les sens des courants tiennent compte des valeurs numériques (\(E_2 > E_1\)).
\(\displaystyle{\begin{array}{lll}V_A-V_B&=&E_2-(r_2+R_5).I_2\\&=&R_4.I_4\\&=&E_1+(r_1+R_3).I_1\end{array}}\)
En posant \(V_B = 0\)
\(\displaystyle{\begin{array}{lll}I_2&=&\frac{E_2-V_A}{r_2+R_5}\\I_4&=&\frac{V_A}{R_4}\\I_1&=&\frac{V_A-E_1}{r_1+R_3}\end{array}}\)
Loi aux noeuds : \(I_2 = I_1 + I_4\)
\(\displaystyle{\frac{E_2-V_A}{r_2+R_5}=\frac{V_A-E_1}{r_1+R_3}+\frac{V_A}{R_4}}\)
\(\displaystyle{\begin{array}{lll}\frac{E_2}{r_2+R_5}+\frac{E_1}{r_1+R_3}&=&V_A(\frac{1}{r_2+R_5}+\frac{1}{r_2+R_3}+\frac{1}{R_4})\\&=&R_4.I_4(\frac{1}{r_2+R_5}+\frac{1}{r_2+R_3}+\frac{1}{R_4})\end{array}}\)
\(\displaystyle{\begin{array}{lll}I_4&=&\frac{\frac{E_2}{r_2+R_5}+\frac{E_1}{r_1+R_3}}{R_4(\frac{1}{r_2+R_5}+\frac{1}{r_2+R_3}+\frac{1}{R_4})}\\I_4&=&0,62\textrm{ A}\end{array}}\)
Question
Méthode : Transformation de Thévenin
Aide simple
Penser à enlever \(R_4\) avant de transformer le circuit.
Rappel de cours
Voir la page Théorème de Thevenin
Solution simple
\(I_4 = 0,62 \textrm{ A (de A vers B)}\)
Solution détaillée
Méthode : Transformation de Thévenin
La f.é.m. E du générateur de Thévenin équivalent au réseau vu de \(A \textrm{ et }B\) est égale à la tension \(V_A - V_B\) à vide, donc en l'absence de \(R_4\) :
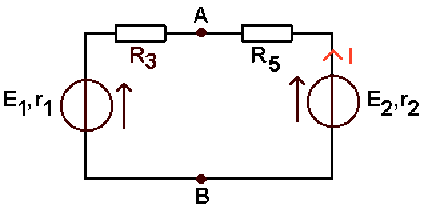
équivalent à :
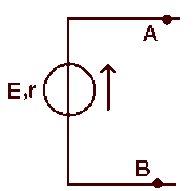
Soit I l'intensité du courant circulant dans la maille
\(\displaystyle{\begin{array}{lll}V_A-V_B&=&E_2-(r_2+R_5).I\\&=&E_1+(r_1+R_3).I\end{array}}\)
\(\displaystyle{I=\frac{E_2-E_1}{r_1+R_3+r_2+R_5}=\frac{7}{30}\textrm{ A}}\)
\(\displaystyle{E=V_A-V_B=\frac{31}{3}\textrm{ V}}\)
La résistance interne de ce générateur de Thévenin est égale à la résistance de l'ensemble \(r_1, R_3, r_2, R_5 \textrm{ vu de A et B }\)
Cet ensemble comporte deux branches en parallèle, la branche de gauche contenant \(r_1 \textrm{ et }R_3,\) la branche de droite formée de \(r_2 \textrm{ et }R_5\).
\(\displaystyle{r=R_{AB}=\frac{1}{\frac{1}{r_1+R_3}+\frac{1}{r_2+R_5}}=\frac{20}{3}\;\Omega}\)
d'où : \(\displaystyle{I_4=\frac{E}{r+R_4}=0,62\textrm{ A}}\)
Question
Méthode : Transformation de Norton
Aide simple
Penser à remplacer \(R_4\) par un court-circuit.
Utiliser les courants de maille dans les mailles de gauche et de droite, ou le théorème de superposition, ce qui revient au même dans ce cas particulier.
Rappel de cours
Voir la page Théorème de Norton
Solution simple
\(\displaystyle{I_4=0,62\textrm{ A(de A vers B)}}\)
Solution détaillée
Méthode : Transformation de Norton
Calcul du courant de court-circuit :
Le courant de court-circuit \(I_0\) est la somme des courants de maille\( I_1 \textrm{ et }I_2\), qui sont aussi les courants qui passeraient dans le court-circuit si le réseau était alimenté par \(E_1\), puis par \(E_2\) (rappel : la conductance d'un court-circuit est infinie).
A cause du court-circuit, \(V_B - V_A = 0\), donc dans la maille de gauche, la loi des mailles donne :
\(\displaystyle{E_1-(r_1+R_3)I_1=0\quad I_1=\frac{E_1}{r_1+R_3}}\)
de même à droite :
\(\displaystyle{E_2-(r_2+R_5)I_2=0\quad I_2=\frac{E_2}{r_2+R_5}}\)
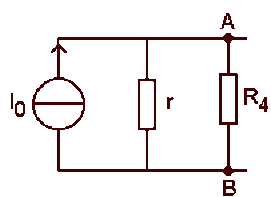
D'où le courant de court-circuit du générateur de Norton équivalent au circuit de \(A \textrm{ vers }B\).
\(\displaystyle{I_0=I_1+I_2=\frac{E_1}{r_1+R_3}+\frac{E_2}{r_2+R_5}=1,55\textrm{ A}}\)
Calcul de la conductance interne vue de \(A \textrm{ et }B\)
L'ensemble \(r_1, R_3, r_2, R_5\) est équivalent à un dipôle unique de conductance \(G_{AB}\) telle que :
\(G_{AB} = \frac{1}{r_{1} + R_{3}} + \frac{1}{r_{2}+R_{5}} = \frac{3}{20} = 0,15 \textrm{ S }\) (loi d'association en parallèle)
Pour \(R_4\), tout se passe comme si le montage était :
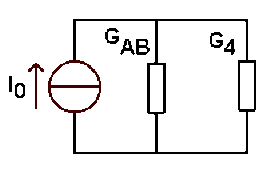
D'où :
\(\displaystyle{I_4=I_0.\frac{G_4}{G_{AB}+G_4}=0,62\textrm{ A}}\)
Question
Méthode : Théorème de superposition après transformation de Norton
Aide simple
Dans le circuit de départ, remplacer les branches contenant les 2 générateurs de tension par des générateurs de courants équivalents ; montrer que la branche de résistance \(R_4\) peut être considérée comme alimentée par un générateur unique, dont on donnera les caractéristiques ; en déduire \(I_4\).
Solution simple
\(\displaystyle{I_4=0,62\textrm{ A (de A vers B)}}\)
Solution détaillée
Théorème de superposition après transformation de Norton:
Générateur de courant équivalent à la branche gauche
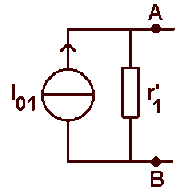
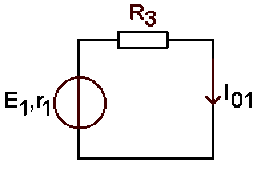
Un court-circuit placé aux bornes de la branche serait parcouru par un courant :
\(\displaystyle{I_{01}=\frac{E_1}{r_1+R_3}=0,8\textrm{ A}}\)
La résistance de cette branche vue de \(A \textrm{ et }B\) est :
\(r'_1 = r_1 + R_3 = 10\;\Omega\)
soit :\( g'_1 = 0,1 \textrm{ S}\)
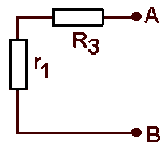
Générateur de courant équivalent à la branche droite.
Un court-circuit placé aux bornes de la branche serait parcouru par un courant :
\(\displaystyle{I_{02}=\frac{E_2}{r_2+R_5}=0,75\textrm{ A}}\)
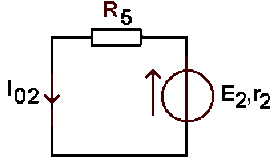
La résistance de cette branche vue de \(A \textrm{ et }B\) est :
\(r'_2 = r_2 + R_5 = 20\;\Omega\)
Soit : \(g'_2 = 0,05 \textrm{ S}\)
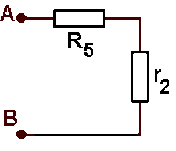
L'association en parallèle est équivalente à un générateur ayant un courant de court-circuit \(I_0 = I_{01} + I_{02} = 1,55 \textrm{ A}\), de conductance \(g = g_1 + g_2 = 0,15\textrm{ S}\), qui débiterait donc dans \(R_4\) un courant :
\(\displaystyle{I_4=I_0.\frac{g_4}{g+g_4}=0,62\textrm{ A}}\)