Calcul d'intensités
Partie
Question
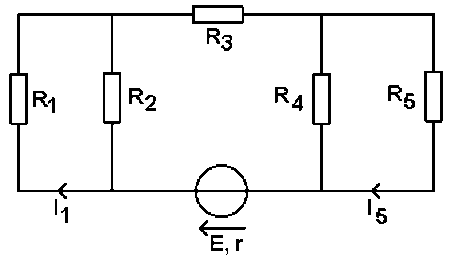
Déterminer les intensités des courants I1 et I5 dans ce circuit :
\(E = 6 \textrm{ V} ; r = 0,5 \Omega ; R_1 = 22 \Omega ; R_2 = 33 \Omega ; R_3 = 100 \Omega ; R_4 = 22 \Omega ; R_5 = 33 \Omega\)
Aide simple
Appliquer la loi des mailles au circuit intérieur et aux circuits extérieurs, puis appliquer la loi des nœuds.
Aide détaillée
Écrire la loi des mailles pour la maille centrale, puis les mailles latérales ; en utilisant ces deux dernières et la loi des nœuds, se ramener à deux équations ayant pour seule inconnue \(I_1\), puis \( I_5\).
Solution simple
\(I_1 = 27 \textrm{ mA}\)
\(I_5 = 18 \textrm{ mA}\)
Solution détaillée
Soient :
I l'intensité débitée par le générateur
\(I_1, I_2, I_3, I_4, I_5\) les intensités des courants traversant \(R_1, R_2, R_3, R_4, R_5\).
Pour la maille centrale : \(E - r.I - R_2.I_2 - R_3.I_3 - R_4.I_4 = 0\; (1)\)
Pour la maille de gauche : \(R_1.I_1 - R_2.I_2 = 0\; (2)\)
Pour la maille de droite : \(R_4.I_4 - R_5.I_5 = 0 \;(3)\)
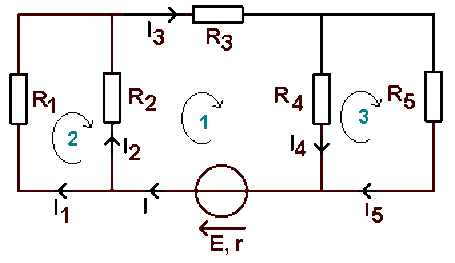
En suivant le circuit dans le sens des aiguilles d'une montre, la loi des noeuds donne :
\(I = I_1 + I_2 = I_3 = I_4 + I_5 \;(4)\)
\((2)\Rightarrow\displaystyle{I_2=\frac{R_1}{R_2}.I_1\Rightarrow I=I_1.\frac{R_1+R_2}{R_2}\;(5)}\)
\(\displaystyle{(3)\Rightarrow I_4=\frac{R_5}{R_4}.I_4\Rightarrow I=I_5.\frac{R_4+R_5}{R_5}\;(6)}\)
\(\displaystyle{(5)(6)\Rightarrow I_1=I_5.\frac{R_2.(R_4+R_5)}{R_5.(R_1+R_2)};I_5=I_1.\frac{R_5.(R_1+R_2)}{R_2.(R_4+R_5)}(7)}\)
On peut donc exprimer (1) en fonction de \(I_1\) :
\(\displaystyle{E-r.I_1.\frac{R_1+R_2}{R_2}-R_1.I_1-R_3.I_1.\frac{R_1+R_2}{R_2}-\frac{R_5^2.(R_1+R_2)}{R_2.(R_4+R_5)}.I_1=0}\)
d'où :
\(\displaystyle{I_1=\frac{E}{\frac{(r+R_3)R_1+R_2}{R_2}+R_1+\frac{R_5^2(R_1+R_2)}{R_2(R_4+R_5)}}=\frac{6}{222,5}=27\textrm{ mA}}\)
et la relation (7) donne : \(I_5=18\textrm{ mA}\)