Générateur équivalent à un réseau
Partie
Question
Calculer les caractéristiques d'un générateur équivalent au circuit ci-contre, vu de \(A \textrm{ et }B\).
\(E = 30 \textrm{ V} ; R_1 = 5 \;\Omega ; R_2 = 45 \;\Omega ; R_3 = 22\;\Omega ; R_4 = 54\;\Omega ; R_5 = 22,5 \;\Omega\)
Aide simple
Utiliser alternativement les deux transformations.
Aide détaillée
Utiliser le modèle de Norton pour associer au générateur un dipôle en parallèle, le modèle de Thévenin pour associer un dipôle en série.
Solution simple
\(E' = 18 \textrm{ V} ; r = 40\;\Omega (\textrm{Thévenin})\)
\(I_0 = 0,45 \textrm{ A}; g = 1/40 \textrm{ S (Norton)}\)
Solution détaillée
L'ensemble \(E, R_1\) est un générateur de Thévenin.
\(R_2\) est aux bornes de cet ensemble : il faut utiliser le modèle de Norton.
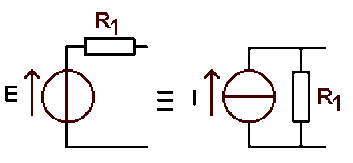
\(\displaystyle{I=\frac{E}{R_1}=6\textrm{ A}}\)
En \(y\) associant \(R_2\) :
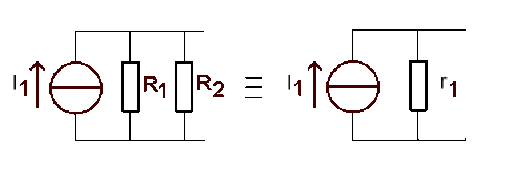
\(\displaystyle{r_1=4,5\;\Omega}\)
\(\displaystyle{\frac{1}{r_1}=\frac{1}{R_1}+\frac{1}{R_2}}\)
\(R_5\) est en série avec cet ensemble : il faut utiliser le modèle de Thevenin
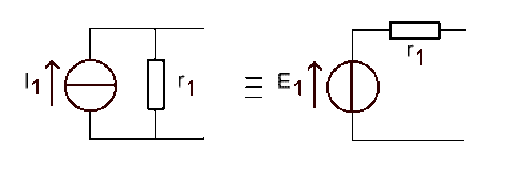
\(\displaystyle{E_1=r_1.I_0=27\textrm{ V}}\)
En y associant \(R_5\)
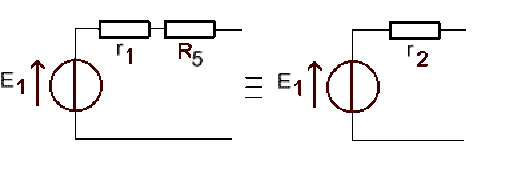
\(r_2 = r_1 + R_5 = 27 \;\Omega\)
\(R_4\) est aux bornes de cet ensemble : il faut repasser au modèle de Norton :
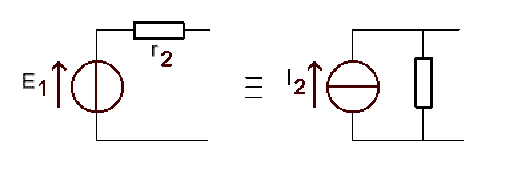
\(\displaystyle{I_2=\frac{E_1}{r_2}=1\textrm{ A}}\)
En y associant \(R_4\) :
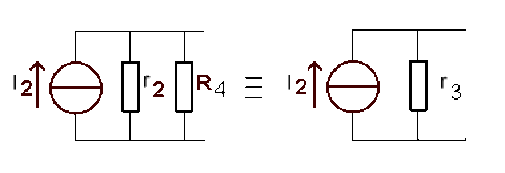
\(\displaystyle{\frac{1}{r_3}=\frac{1}{r_2}+\frac{1}{R_4}=18\;\Omega}\)
Il reste à associer \(R_3\) en série avec ce générateur. Le modèle de Thévenin est donc le mieux adapté.
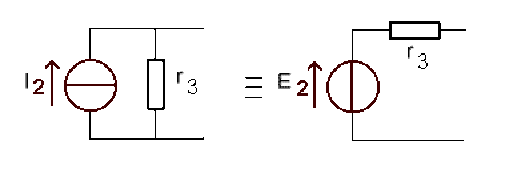
\(\displaystyle{E_2=r_3.I_2=18\textrm{ V}}\)
En y associant \(R_3\)
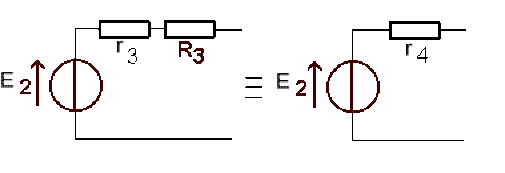
\(r_4 = r_3 + R_3 = 40 \;\Omega\)
dont le modèle de Norton est :
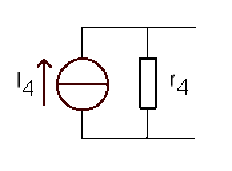
\(\displaystyle{I_3=\frac{E_2}{r_4}=0,45\textrm{ A}}\)
\(\displaystyle{g_4=\frac{1}{r_4}=\frac{1}{40}\textrm{ S}}\)