Générateur de Norton (4)
Partie
Question
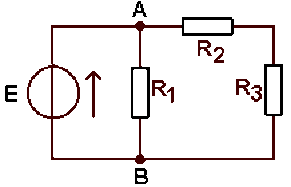
Déterminer les caractéristiques du générateur de Norton équivalent au réseau ci-dessous, vu de \(A \textrm{ et }B\) :
Application numérique : \(E = 30 \textrm{ V} ; R_1 = 100 \;\Omega ; R_2 = 470 \;\Omega ; R_3 = 330 \;\Omega\)
Aide simple
Le générateur de Norton est caractérisé par :
Le courant \(I_{cc}\) qui passerait dans un court-circuit placé entre \(A \textrm{ et }B\).
Une résistance interne qui est la résistance du réseau passif vu de \(A \textrm{ et }B\).
Aide détaillée
La conductance de branches en parallèle est égale à la somme des conductances
La conductance d'un dipôle de résistance nulle est infinie.
Solution simple
\(I _{\infty}=\infty\)
\(r = 0\)
Solution détaillée
Si on place entre \(A \textrm{ et }B\) un court-circuit, le générateur débite dans une conductance infine :
\(I_{\infty}=g.E=\infty\)
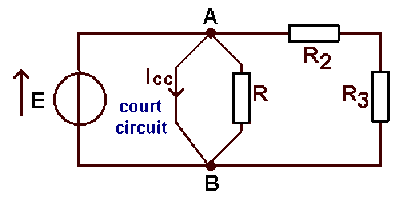
équivalent à :
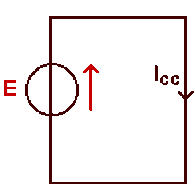
Quand un court-circuit est en parallèle sur une résistance, la résistance équivalente est nulle.
Donc, vu de\( A \textrm{ et }B\), le réseau, dans lequel on a remplacé \(E\) par un court-circuit, a une résistance nulle.
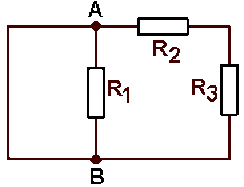
équivalent à :
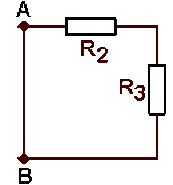
equivalent à :
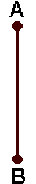
Le schéma de Norton équivalent au réseau vu de \(A \textrm{ et }B\) est un générateur de résistance interne nulle pouvant théoriquement débiter une intensité infinie.