Calcul algébrique d'une intensité [Analyse des réseaux linéaires]

Calcul algébrique d'une intensité

Partie

Question

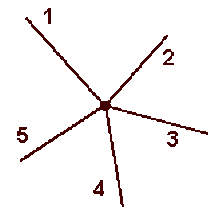
Donner la valeur algébrique de l'intensité manquante :

a) $I_1 = 1 \textrm{ A} ; I_2 = -2 \textrm{ A} ; I_3 = -5 \textrm{ A} ; I_4 = ? \textrm{ A} ; I_5 = 10 \textrm{ A}$

b) $I_1 = 10 \textrm{ A} ; I_2 = 8 \textrm{ A} ; I_3 = -5 \textrm{ A} ; I_4 = -2 \textrm{ A} ; I_5 = ? \textrm{ A}$

c) $I_1 = -5 \textrm{ A} ; I_2 = 4 \textrm{ A} ; I_3 = ? \textrm{ A} ; I_4 = -2 \textrm{ A} ; I_5 = 1 \textrm{ A}$

Aide simple

Aide détaillée

Solution simple

a) $I_4 = -4 \textrm{ A}$ ;

b) $I_5 = -11 \textrm{ A}$ ;

c) $I_3 = 2 \textrm{ A}$ ;

Solution détaillée

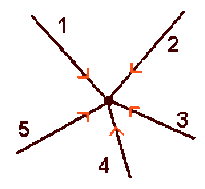
En un noeud d'un réseau, la somme algébrique des intensités des courants dans l'ensemble des branches est nulle ; donc, en comptant positivement les courants allant vers le noeud :

a) $I_4 = - (I_1 + I_2 + I_3 + I_5) = - (1 - 2 - 5 + 10) = -4 \textrm{ A}$ ; ce courant s'écarte du noeud

b) $I_5 = - (I_1 + I_2 + I_3 + I_4) = - (10 + 8 - 5 - 2) = -11 \textrm{ A}$ ; ce courant s'écarte du noeud

c) $I_3 = - (I_1 + I_2 + I_4 + I_5) = - (-5 + 4 -2 + 1) = 2 \textrm{ A}$ ; ce courant va vers le noeud