Cas d'une particule libre
Durée : 9 mn
Note maximale : 9
Question
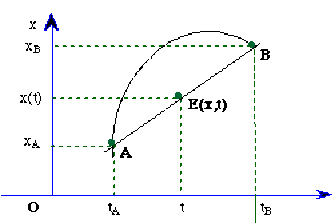
Parmi tous les chemins qui relient deux points \(A\) et \(B\) de l'espace-temps, l'un est appelé "chemin réel" car il correspond au mouvement d'un point matériel tel qu'il est décrit par la Loi Fondamentale de la Dynamique. Le long des autres, qu'on appelle "virtuels", la Loi Fondamentale n'est pas satisfaite.
Dans le cas d'un point matériel libre dans l''espace-temps à deux dimensions \(( x , t )\), vérifiez que le "chemin réel" entre deux points \(A\) et \(B\) de l'espace-temps est le "segment de droite \(AB\)". Quelle est la trajectoire ? Quelle est la vitesse ?
Montrer que la grandeur
\(\displaystyle{S_AB=\int_A^Bv^2dt}\)
est minimale le long du chemin réel. On utilisera l'inégalité : \(<v^2>\ge<v>^2\), où le symbole \(< >\) désigne la valeur moyenne temporelle : par exemple la vitesse moyenne s'écrit :
\(<v>=\frac{\left(\int_{t_A}^{t_B}v dt\right)}{(t_B-t_A)}\)
Solution
La trajectoire est le segment de l'axe \(Ox\) situé entre \(x_A\) et \(x_B\).
(1 point)
Le long du "segment de droite \(AB\)" la vitesse ( c'est à dire la pente de la courbe \(x = f(t)\) ) est constante, \(v(t) = v_0\) et \(\displaystyle{v_0=\frac{(x_B-x_A)}{(t_B-t_A)}}\)
(1 point)
Le long de tous les autres chemins, la vitesse \(v(t)\) varie mais on a toujours \(<v>=0\). Le mouvement est donc uniforme, ce qui correspond bien à un point matériel libre sur l'axe \(Ox\), et le segment de droite \(AB\) est bien le "chemin réel" entre les deux points \(A\) et \(B\) de l'espace-temps. Les autres chemins, le long desquels la vitesse est variable, ne correspondent à aucun mouvement réel pour un point matériel libre : ils sont donc "virtuels".
(2 points)
On peut écrire
\(\displaystyle{S_AB=\int_A^Bv^2dt=(t_B-t_A)<v^2>}\)
en utilisant la définition de la moyenne de \(v^2\), et comme
\(<v^2>\ge<v>^2\)
on déduit que :
\(\displaystyle{S_AB\ge(t_B-t_A)<v^2>}\)
(2 points)
Enfin comme \(<v>=v_0\) le long de tous les chemins, on obtient :
\(\displaystyle{S_AB\ge(t_B-t_A)<{v_0}^2>}\)
(1 point)
De l'expression intégrale de \(S_{AB}\) on déduit que l'inégalité est réalisée seulement lorsque \(v(t) = v_0\), c'est à dire précisément le long du "chemin réel".
(2 points)