Mouvement circulaire uniforme : vitesse
Durée : 6 mn
Note maximale : 6
Question
Par rapport à un référentiel terrestre, la Lune ( assimilée à un point matériel) décrit une trajectoire circulaire d'un mouvement uniforme de vitesse \(V\).
Déterminez la direction et le sens du vecteur vitesse moyenne entre deux instants successifs \(t\) et \(t'\).
Utilisez la géométrie pour déterminez la direction et le sens du vecteur vitesse moyenne lorsque l'intervalle de temps \(t'- t\) est infiniment petit.
Déterminez le vecteur vitesse instantanée en tout point de la trajectoire.
Solution
Soient \(M\) et \(M'\) les positions de la Lune à deux instants successifs, \(t\) et \(t'\), sur la trajectoire circulaire dont la Terre est le centre \(C\).
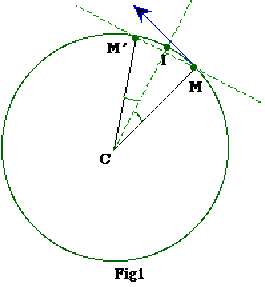
Le vecteur vitesse moyenne entre ces deux instants est \(\frac{\vec{MM'}}{(t'-t)}\)
il est porté par la droite \(MM'\) et est dirigé dans le sens du mouvement.
(2 points)
Le segment de droite \(MM'\) (qui est une "corde") est la base d'un triangle isocèle \(MCM'\): \(MM'\) est donc perpendiculaire à la bissectrice \(CI\) de l'angle \((CM, CM')\) qui est aussi la médiatrice de \(MM'\).
(1 point)
La longueur de l'arc \(MM'\) est donnée par : \(MM' = V(t' - t)\). Ainsi, lorsque \(t'- t\) est infiniment petit le point \(M'\) est infiniment voisin de \(M\) : il en est de même du point \(I\) qui est au milieu de l'arc \(MM'\).
(1 point)
La vitesse instantanée est, par définition, la limite de la vitesse moyenne :
\(\vec{v}(t)=\lim_{(\Delta t\rightarrow0)}\frac{\vec{MM'}}{dt}\)
Le vecteur \(\vec{v}(t)\), de norme \(V\), est donc dirigé suivant la droite perpendiculaire au rayon \(CM\) ( limite de \(CI\) lorsque \(dt\) tend vers 0) et orienté dans le sens du mouvement.
On vérifie qu'il est bien tangent à la trajectoire au point \(M\).
(2 points)