Distances focales
Définition : Distance focale objet et Distance focale image
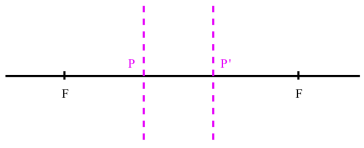
Considérons un système centré caractérisé par ses foyers objet F et image F' et par ses plans principaux P et P'. La valeur algébrique du segment PF est appelée distance focale objet f tandis que la valeur algébrique du segment P'F' est appelée distance focale image f ' .
Nous allons déterminer la relation qui existe entre f et f'.
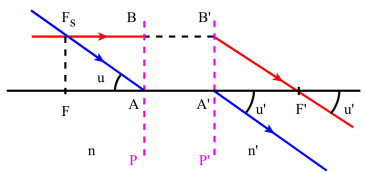
Soient n l'indice du milieu dans lequel est placé l' objet [1]et n' l'indice du milieu dans lequel se trouve l' image [2]. Un objet AB placé dans le plan principal objet P a pour image A'B' placée dans le plan principal image P'.
Un rayon incident parallèle à l'axe et passant par B émerge suivant B'F' incliné d'un angle u' par rapport à l'axe du système.
Soit Fs le foyer objet [3]secondaire intersection du rayon incident parallèle à l'axe et passant par B avec le plan focal objet.
Au rayon incident FsA correspondra un émergent passant par A' et parallèle à B'F' donc incliné d'un angle u' par rapport à l'axe.
Appliquons la relation de Lagrange-Helmholtz : \(\mathrm n~.~\overline{\mathrm{AB}}~.~\mathrm u=\mathrm n{\mathrm'}~.~\overline{\mathrm A{\mathrm'}\mathrm B{\mathrm'}}~.~\mathrm u{\mathrm'}\) et par définition des plans principaux :
\(\overline{\mathrm{AB}}=\overline{\mathrm A{\mathrm'}\mathrm B{\mathrm'}}\) on en déduit donc : \(\mathrm n~\mathrm u=\mathrm{n'}~\mathrm{u'}\)
Si l'on compte positivement les angles dans le sens trigonométrique on a :
\(\tan~\mathrm u\approx\mathrm u=-\frac{\overline{\mathrm{FF}_{\mathrm s}}}{\overline{\mathrm{FA}}}~\) et \(~\tan~\mathrm{u'}\approx\mathrm{u'}=-\frac{\overline{\mathrm{A'B'}}}{\overline{\mathrm{F'A'}}}\)
\(\overline{\mathrm{FA}}=\overline{\mathrm{FP}}=-\mathrm f~\) et \(~\overline{\mathrm{F'A'}}=\overline{\mathrm{F'P'}}=-\mathrm{f'}\)
on en déduit : \(\mathrm f~\mathrm u=-\mathrm{f'}~\mathrm{u'}\) et la relation reliant f, f', n et n' :
\(\frac{\mathrm{f'}}{\mathrm f}=-\frac{\mathrm{n'}}{\mathrm n}\)
On déduit de cette relation que les distances focales sont toujours de signe opposé et que si les milieux extrêmes sont identiques (même indice) les distances focales objet et image sont égales.
La vergence d'un système centré sera définie par :
\(\mathrm V=\frac{\mathrm{n'}}{\mathrm{f'}}=-\frac{\mathrm n}{\mathrm f}\)
La distance focale s'exprime en mètres et la vergence en dioptries.
Le sens positif le long de l'axe étant pris selon le sens de propagation de la lumière, lorsque la vergence sera positive le système sera convergent alors qu'il sera divergent pour une vergence négative.