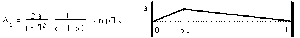Corde pincée
Partie
Question
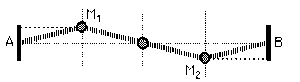
Une corde de longueur \(L\) et de masse linéique \(\rho\) est tendue entre \(2\) points fixes \(A\) et \(B\) avec une tension \(T\) . On se propose d'étudier les oscillations de cette corde à partir des conditions initiales suivantes :
la corde est pincée en \(M_1\) \(( z_1 = \frac{L}{4})\) et en \(M_2\) \((z_2 =\frac{3L}{4})\) de sorte que :
\(\psi(z_1, 0)=-\psi(z_2, 0)=a_0\)
les points \(M_1\) et \(M_2\) sont ensuite relâchés sans vitesse initiale, de sorte que :
\(\forall z, \psi'(z,0)=0\)
Dans toute la suite, on posera \(a_0 << L\) et on admettra que la tension \(T\) est assez grande pour pouvoir négliger le poids de la corde.
Remarque préliminaire :
La configuration initiale \(\psi(z, 0)\) peut se représenter comme somme des 2 configurations initiales \(\phi_1(z, 0)\) et \(\phi_2(z, 0)\).
Les amplitudes d'oscillations seront notées par la suite :
\(\psi(z,t)\) si la corde oscille à partir de l'état initial \(\psi(z, 0)\)
\(\phi_1(z,t)\) si la corde oscille à partir de l'état initial \(\phi_1(z, 0)\)
\(\phi_2(z,t)\) si la corde oscille à partir de l'état initial \(\phi_2(z, 0)\)
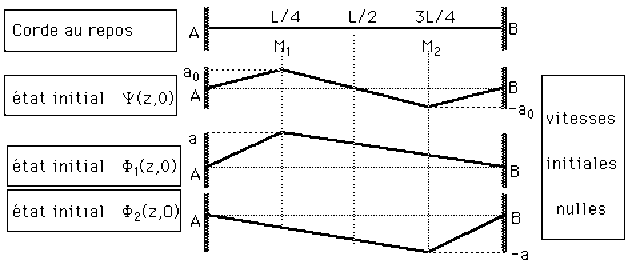
1- Déterminer la relation entre \(a\) et \(a_0\) pour que l'on ait :
\(\psi(z,0) = \phi_1(z, 0) + \phi_2(z, 0)\)
2- En utilisant la description de ces états vibratoires par superpositions des modes propres de la corde, montrer que :
\(\forall t, \psi(z,t) = \phi_1(z,t) + \phi_2(z,t)\)
3- Exprimer \(\phi_1(z, 0)\) en fonction des coefficients de Fourier \(A_{1p}\) ainsi que \(\phi_2(z, 0)\) en fonction des coefficients de Fourier \(A_{2p}\).
4- Montrer que : \(\phi_1(z,0)=-\phi_2(L-z, 0)\).
5- En déduire deux relations entre \(A_{1p}\) et \(A_{2p}\) valables respectivement : l'une pour \(p\) pair, l'autre pour \(p\) impair.
6- Donner alors l'expression de \(\psi(z,0)\) en fonction des \(A_{1p}\).
Préciser quelles valeurs de \(p\) interviennent.
7- Tenant compte de la question \(2\), donner l'amplitude \(\psi(z,t)\) de la vibration à l'instant \(t\).
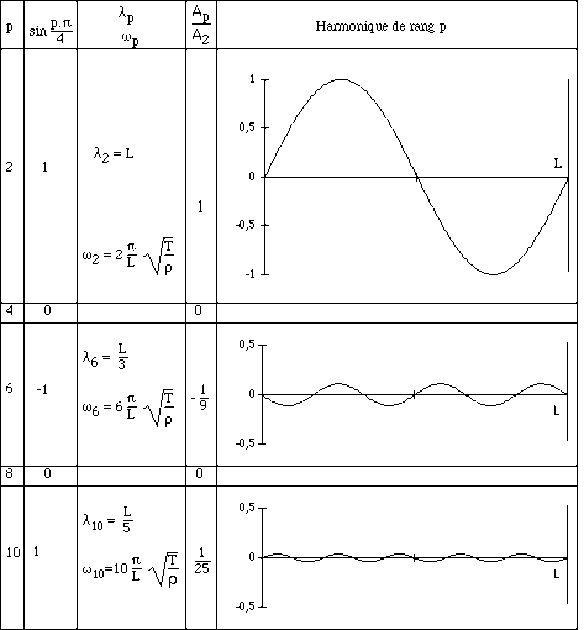
8- On rappelle que pour une corde de longueur \(L\) pincée initialement à l'abscisse \(a_L\), l'amplitude de l'harmonique de pulsation \(\omega_p\) est :
En déduire l'expression de \(A_{1p}\).
Indiquer sur un tableau, pour les valeurs successives de \(p\) intervenant dans \(\psi(z,0)\) :
les valeurs correspondantes de \(A_{1p}\) (en se limitant aux \(3\) premières valeurs non nulles)
les valeurs correspondantes de \(\omega_p\). Indiquer sur ce même tableau, pour ces premiers harmoniques, le rapport de leurs amplitudes avec le fondamental. Dessiner approximativement, mais à la même échelle et en valeur algébrique, les trois premiers termes de \(\psi(z,0)\).
9- La corde pincée initialement selon \(\psi(z,0)\) va-t-elle vibrer selon un mode propre ?
Quel autre système physique simple déformé initialement de cette même façon vibrerait ultérieurement selon un mode propre ?
Comparer la pulsation du mode propre ainsi obtenu pour ce dernier système à la pulsation du fondamental relatif à la corde pincée.
Conclure.
Rappel de cours
Voir la page Mise en équation
Solution détaillée
La corde de longueur \(L\) et de densité linéique de masse \(\rho\) est tendue entre \(2\) les points fixes \(A\) et \(B\) avec une tension \(T\).
La corde est pincée en \(M_1\) (\(z_1 =\frac{L}{4}\)) et en \(M_2\) (\(z_2 =\frac{3L}{4}\)) de sorte que : \(\psi(z_1 , 0) = - \psi(z_2 , 0) = a_0\)
Les points \(M_1\) et \(M_2\) sont ensuite relâchés sans vitesse initiale, de sorte que : \(\forall z, \dot{\psi}(z,0)=0\)
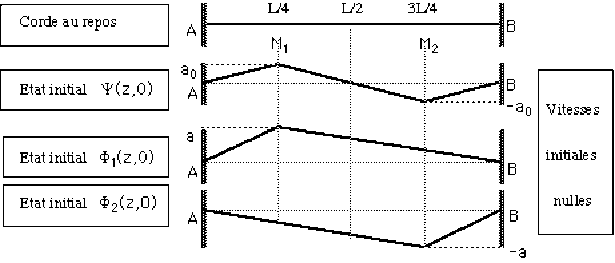
1-
La relation (1) : \(\psi(z,0) = \phi_1(z,0) + \phi_2(z,0)\), nécessite en particulier en \(z=\frac{L}{4}\) :
\(\psi(\frac{L}{4}, 0)=\phi_1(\frac{L}{4},0)+\phi_2(\frac{L}{4},0)\)
avec : \(\psi(\frac{L}{4},0)=a_0, \phi_1(\frac{L}{4},0)=a\) et \(\phi_2(\frac{L}{4},0)=-\frac{a}{3}\Rightarrow a=\frac{3}{2}a_0\)
Cette égalité est suffisante pour que soit satisfaite la relation (1) en \(M_1\) et en \(M_2\).
Donc, la relation (1) est satisfaite en \(z = 0\), en \(z = z_1\), en \(z = z_2\) et en \(z = L\), c'est à dire aux limites des 3 domaines de variation des fonctions considérées. Par ailleurs, sur chacun de ces 3 domaines, les 3 fonctions considérées sont linéaires.
\(\Rightarrow\) la relation linéaire (1) est donc satisfaite \(\forall z\).
2-
Si cette corde est dans un état initial représenté par la fonction \(\phi_p(z,0) = \sin K_pz\), elle se met en vibration selon la fonction : \(\phi_p(z,t) = sin (K_p.z) cos (\omega_p.t + a_p)\) [mode propre \(p\)].
Si la corde est dans un état initial représenté par la fonction \(\phi_1(z,0)=\displaystyle{\sum_{p=1}^{p=\infty}A_{1p}\sin(K_pz)}\), chacun de ces termes vibrera selon la fonction \(\phi_p(z,t)\) correspondante, et donc (par raison de linéarité) la corde vibrera selon la fonction :
\(\phi_1(z,0)=\displaystyle{\sum_{p=1}^{p=\infty}A_{1p}\sin(K_pz)\cos(\omega_pt+\alpha_p)}\).
Même argument : la corde dans un état initial représenté par la fonction \(\phi_2(z,0)\) vibrera selon la fonction :
\(\phi_2(z,0)=\displaystyle{\sum_{p=1}^{p=\infty}A_{2p}\sin(K_pz)\cos(\omega_pt+\alpha_p)}\).
Noter que, dans ces 2 décompositions, il s'agit des mêmes fonctions \(\sin(K_pz)\) et des mêmes pulsations propres, car il s'agit du même système physique (simplement lâché dans des états initiaux différents) dont l'état est représenté sur la base de ses modes propres.
Par raison de linéarité (toujours), le système lâché dans un état initial représenté par la somme : \(\psi(z, 0) = \phi_1(z, 0) + \phi_2(z, 0)\) évoluera donc, au cours du temps, selon la somme des fonctions représentant l'évolution de chacun des termes, soit :
\(\psi(z,t)=\phi_1(z,t)+\phi_2(z,t)=\displaystyle{\sum_{p=1}^{p=\infty}(A_{1p}+A_{2p})\sin(K_pz)\cos( \omega_pt+\alpha_p)}\) \(\forall t\)
soit : \(\psi(z,t)=\displaystyle{\sum_{p=1}^{p=\infty} \mathcal A_p \sin(K_pz)\cos( \omega_pt+\alpha_p)}\) avec \(\mathcal A_p=A_{1p}+A_{2p}\)
3-
On peut dire également que l'expression \(\psi(z,0)=\displaystyle{\sum_{p=1}^{p=\infty}(A_{1p}+A_{2p})\sin(K_pz)}\), définie pour \(z \in\) \([O, L]\), coïncide sur l'intervalle \([O, L]\) avec la décomposition en série de Fourier, de la forme initiale de la corde représentée par son prolongement périodique (\(z\) variant alors de \(-\infty\) à \(+\infty\)).
Pour pouvoir parler du développement en série de Fourier d'une fonction il est nécessaire que cette fonction soit périodique : c'est la raison pour laquelle on doit considérer le prolongement périodique de la corde et non pas la corde proprement dites délimitée par l'intervalle \([0, L]\).
Si \(\phi_1(z,0)\) est maintenant le prolongement périodique de la forme antérieurement appelée \(\phi_1(z,0)\), dans les \(2\) cas les coefficients \(A_{1p}\) de la décomposition devront avoir la même valeur pour pouvoir donner sur \([O, L]\) le même résultat, car le prolongement de la fonction doit coïncider avec la fonction sur son support \([O, L]\).
De même, si \(\phi_2(z,0)\) est maintenant le prolongement périodique de la forme antérieurement appelée \(\phi_2(z,0)\), les coefficients de Fourier \(A_{2p}\) sont ceux de la décomposition sur la base des modes propres.
Le prolongement périodique effectué n'est (bien sûr) pas quelconque : la période \(\lambda_1\) du prolongement est la plus grande possible qui satisfasse les conditions aux limites du système (à savoir ici : extrémités fixes).
Donc ici : \(\lambda_1=2L\), et \(K_1=\frac{2\pi}{\lambda_1}=\frac{\pi}{L}\) donnent le développement :
\(\phi_1(z,0)=\displaystyle{\sum_{p=1}^{p=\infty}A_{1p}\sin(K_pz)}\) et \(\phi_2(z,0)=\displaystyle{\sum_{p=1}^{p=\infty}A_{2p}\sin(K_pz) \textrm{ avec } K_p=pK_1=p\frac{\pi}{L}}\)
4-
Les formes \(\phi_1(z,0)\) et \(\phi_2(z,0)\) sont symétriques par rapport au point milieu du segment \(AB\). (revoir le schéma précédent) Le point d'abscisse \(z\) sur \(AB\) a pour symétrique sur \(AB\) le point d'abscisse \((L-z)\).
En des points symétriques par rapport au milieu de \(AB\), les amplitudes respectives de \(\phi_1\) et de \(\phi_2\) sont donc égales et opposées, soit : \(\phi_1(z,0) = - \phi_2(L-z, 0)\)
5-
On a donc : \(\phi_1(z,0)=\displaystyle{\sum_{p=1}^{p=\infty}A_{1p}\sin(K_pz)=-\phi_2(L-z,0)= -\displaystyle{\sum_{p=1}^{p=\infty}A_{2p}\sin(K_p(L-z))}}\)
avec : \(\sin(K_p(L-z))=\sin(K_pL-K_pz)=\sin(p \pi-K_pz)\).
On doit distinguer les \(2\) cas :
\(p\) pair\(\Rightarrow \sin(p \pi-K_pz)=-\sin(K_pz)\)
\(p\) impair \(\Rightarrow \sin(p \pi-K_pz)=+\sin(K_pz)\)
\(\Rightarrow \phi_2(L-z,0)=\displaystyle{\sum_{\textrm{p impair}}A_{2p}\sin(K_pz)-\displaystyle{\sum_{\textrm{p pair}}A_{2p}\sin(K_pz)}}\)
\(\phi_1(z,0)=\displaystyle{\sum_{\textrm{p impair}}A_{1p}\sin(K_pz)+\displaystyle{\sum_{\textrm{p pair}}A_{1p}\sin(K_pz)}}\)
En faisant la somme : \(0= \displaystyle{\sum_{\textrm{p impair}}(A_{1p}+A_{2p})\sin(K_pz)+\displaystyle{\sum_{\textrm{p pair}}(A_{1p}-A_{2p})\sin(K_pz)}}\)
Cette égalité ne peut être satisfaite que si les coefficients multiplicatifs des fonctions sont tous nuls.
Donc :
\(p\) pair \(\Rightarrow A_{1p}=A_{2p}\)
\(p\) impair \(\Rightarrow A_{1p}=-A_{2p}\)
6-
Pour tous les termes de rang \(p\) pair : \(A_p=A_{1p}+A_{2p}=2A_{1p}\).
Pour tous les termes de rang \(p\) impair : \(A_p=A_{1p}+A_{2p}=0\).
Sachant que : \(\psi(z,0)=\displaystyle{\sum_{p=1}^{p=\infty}(A_{1p}+A_{2p})\sin(K_pz)}\)
il vient : \(\psi(z,0)=\displaystyle{\sum_{\textrm{p pair}}2A_{1p}\sin(K_pz)}\) (somme sur toutes les valeurs paires de \(p=2\) à l'infini)
Remarquer que tous les termes de rang impair possèdent une symétrie par rapport à la médiatrice du segment \(AB\), et que les termes de rang pair sont symétriques par rapport au milieu du segment \(AB\).
L'état initial \(\psi(z,0)\) possède une symétrie par rapport au milieu du segment \(AB\) et c'est cette condition qui sélectionne les termes (pairs) intervenant dans le développement.
7-
Tenant compte de la question \(b\), l'amplitude \(\psi(z,t)\) de la vibration à l'instant \(t\) devient :
\(\psi(z,t)=\displaystyle{\sum_{\textrm{p pair}}2A_{1p}\sin(K_pz)\cos(\omega_pt+\alpha_p)}\) \(\forall t\).
La vitesse d'un point quelconque de la corde s'obtient en dérivant cette somme. La dérivée sera donc une combinaison linéaire de termes en \(\sin(\omega_p+\alpha_p)\). Ces termes doivent être nuls en \(t=0\) pour satisfaire la condition initiale sur les vitesses. Cette condition initiale est donc satisfaite en prenant : \(\alpha_p = 0 ~\forall p\).
Finalement : \(\psi(z,t)=\displaystyle{\sum_{\textrm{p pair}}2A_{1p}\sin(K_pz)\cos(\omega_pt)}\)
8-
Sachant que pour une corde de longueur L pincée initialement à l'abscisse \(\alpha_L\), l'amplitude de l'harmonique de pulsation \(\omega_p\) est :
on aura ici, pour la corde pincée à l'abscisse : \(az=\alpha_L=\frac{L}{4}\Rightarrow A_{1p}=\frac{2a}{p^2\pi^2}\frac{4}{3}\sin\frac{p\pi}{4}\)
On notera : \(A_p=2A_{1p}\) les coefficients de \(\psi(z,t)\) (voir le tableau récapitulatif précédent).
Les valeurs de \(\omega_p\) sont déterminées par : \(\omega_p=\frac{p\pi}{L}\sqrt{\frac{T}{\rho}}=p\omega_1\), avec \(\omega_1=\frac{\pi}{L}\sqrt{\frac{T}{\rho}}\)
Pour le premier mode non nul du développement, on a par exemple : \(\omega_2=\frac{2\pi}{L}\sqrt{\frac{T}{\rho}}\)
9-
La corde pincée suivant la forme initiale \(\psi(z,0)\) vibre ensuite selon la combinaison de modes propres définie par la somme :
\(\psi(z,t)=\displaystyle{\sum_{\textrm{p pair}}\mathcal A_p\sin(K_pz)\cos(\omega_pt)}\)
où \(\mathcal A_p=2A_{1p}=\frac{4a}{p^2\pi^2}\frac{4}{3}\sin\frac{p\pi}{4}\) est l'amplitude du mode propre de rang \(p\).
La corde ne vibre donc pas selon un mode propre.On notera cependant que l'amplitude des harmoniques successifs décroit rapidement (\(\mathcal A_p \div \frac{1}{p^2}\)) en fonction de \(p\) \(\Rightarrow\) le premier terme non nul \((p=2)\) de longueur d'onde \(\lambda_2= L\) est donc prépondérant.
Ce système 3 masses 4 ressorts étant symétrique par rapport au centre de \(AB\), il vibre dans le mode propre de rang \(p=2\) : la masse 2 reste immobile et les masses 1 et 3 vibrent avec des amplitudes égales et opposées, et à une pulsation définie (avec \(p=2\) et \(N+3\)) par l'expression générale : \(\Omega_p=2\omega_0\sin\frac{p\pi}{2(N+1)}\)
Noter que la pulsation \(\Omega_2\) du système 3 masses - 4 ressorts est différente de celle \(\omega_2\) de la corde vibrante.
Par contre, si on considérait un système masses-ressorts dans lequel on ferait tendre le nombre de masse \(N\) vers l'infini, alors sa pulsation tendrait vers la limite \(\Omega_p\rightarrow \omega_0\frac{p\pi a}{(N+1)a}=p\omega_0\frac{\pi a}{L}\)
Pour le mode considéré ici : \(\Omega_2\rightarrow 2\frac{\pi}{L}a\sqrt{\frac{T}{m . a}}=2\frac{\pi}{L}\sqrt{\frac{T}{m/a}}\) (on rappelle que \(\omega_0=\sqrt{\frac{T}{m . a}}\))
Sachant que le rapport \(m/a\) peut se définir comme la masse par unité de longueur (ou densité linéique \(\rho\)), on voit que la pulsation \(\Omega_2\) du système \(N \textrm{ masses } - (N+1)\) ressorts tend exactement vers la pulsation \(\omega_2\) du premier terme du développement \(\omega_2=2\frac{\pi}{L}\sqrt{\frac{T}{\rho}}\) lorsque \(N\rightarrow\infty\).