Séries de Fourier et parité

Partie

Question

  1. Soit \(A_n(t)\) une suite de fonctions paires de la variable \(t\) et \(B_n(t)\) une suite de fonctions impaires de \(t\). On considère la fonction de \(t\) définie par :

    \(\psi(t)=\displaystyle{\sum_{n=1}^{n=N}a_nA_n(t)+b_nB_n(t) }\) où \(a_n\) et \(b_n\) sont des coefficients réels non tous nuls.

    Vérifier les propriétés suivantes :

    • la fonction \(\psi_p(t)=\displaystyle{\sum_{n=1}^{n=N}a_nA_n(t)}\) est paire

    • la fonction \(\psi_i(t)=\displaystyle{\sum_{n=1}^{n=N}b_nB_n(t)}\) est impaire

    et réciproquement une fonction \(\psi(t)\) définie par : \(\displaystyle{\sum_{n=1}^{n=N}a_nA_n(t)+b_nB_n(t)}\)

    • se réduit à la forme \(\psi_p(t)\) si la fonction \(\psi(t)\) est paire

    • se réduit à la forme \(\psi_i(t)\) si la fonction \(\psi(t)\) est impaire.

  2. On admettra que cette propriété reste vraie si \(N\) est infini, à condition que ces séries de fonctions convergent.

    Dans ces conditions, écrire les développements en Série de Fourier : d'une fonction \(F\) paire et respectivement d'une fonction \(G\) impaire.

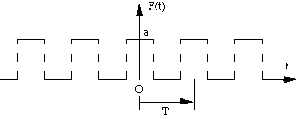
    On considère un phénomène dépendant du temps, \(t \in[-i, +i]\) périodique, de période \(T\), et valant \(+a ~(a > 0)\) pendant une demi période et \(0\) pendant l'autre demi période.

  3. Choisir l'origine des \(t\) de sorte que le phénomène soit représenté par une fonction \(F\) périodique paire. Donner l'expression de la fonction \(F\) et représenter son graphe.

    Exprimer son développement en série de Fourier et calculer les coefficients de ce développement.

    Représenter le spectre de Fourier de \(F\).

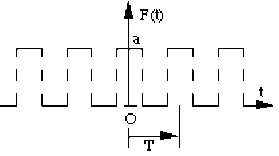
  4. Choisir l'origine des \(t\) de sorte que le phénomène soit représenté par une fonction \(G\) périodique impaire.

    Donner l'expression de la fonction \(G\) et représenter son graphe.

    Exprimer son développement en série de Fourier et calculer les coefficients de ce développement. Représenter le spectre de Fourier de \(G\).

Rappel de cours

Voir la page Parité : exemple du signal carré symétrique

Solution détaillée

1-

On considère la fonction : \(\psi(t)=\displaystyle{\sum_{n=1}^{n=N}a_nA_n(t)+b_nB_n(t)}\)

où \(A_n(t)\) est une suite de fonctions paires \(\Leftrightarrow A_n(t)=A_n(-t)\)

\(B_n(t)\) est une suite de fonctions impaires \(\Leftrightarrow B_n(t)=-B_n(-t)\)

\(\psi_p(t)=\displaystyle{\sum_{n=1}^{n=N}a_nA_n(t)\Rightarrow \psi_p(-t)=\displaystyle{\sum_{n=1}^{n=N}a_nA_n(-t)\equiv\displaystyle{\sum_{n=1}^{n=N}a_nA_n(t) =\psi_p(t)\Leftrightarrow}}}\) paire

\(\psi_i(t)=\displaystyle{\sum_{n=1}^{n=N}b_nB_n(t)\Rightarrow \psi_i(-t)=\displaystyle{\sum_{n=1}^{n=N}b_nB_n(-t)\equiv -\displaystyle{\sum_{n=1}^{n=N}b_nB_n(t) =-\psi_i(t)\Leftrightarrow}}}\) impaire

Toute combinaison linéaire de fonctions paires est une fonction paire.

Toute combinaison linéaire de fonctions impaires est une fonction impaire.

Inversement, une fonction réelle quelconque (ni paire, ni impaire) peut s'exprimer comme combinaison linéaire de fonctions paires et impaires : \(\psi(t) = \psi_p (t) + \psi_i (t)\)

Si \(\psi(t)\) est paire : \(\psi(t)=\psi(-t)\)

\(\Rightarrow \psi_p(t)+\psi_i(t)=\psi_p(-t)+\psi_i(-t)\) et \(\psi_p(t)\) paire \(\Rightarrow \psi_i(t)=\psi_i(-t)\)

\(\Rightarrow \psi_p(t)=\psi_p(-t)\) et \(\psi_i(t)\) impaire \(\Rightarrow \psi_i(-t)=-\psi_i(t) \Rightarrow \psi_i(t)=0\)

Si la fonction \(\psi(t)\) est paire , elle se réduit à une combinaison linéaire \(\psi_p(t)\) de fonctions paires.

On montre de la même façon que si la fonction \(\psi(t)\) est impaire, elle se réduit à une combinaison linéaire \(\psi_i(t)\) de fonctions impaires.

2-

On admet que ce résultat reste vrai si \(N \rightarrow \infty\) et on l'applique au cas des fonctions périodiques :

\(\psi(t)=a_0+\underbrace{\displaystyle{\sum_{n=1}^{\infty}}a_n\cos(\omega_nt)}_{\textrm{termes pairs}}+\underbrace{\displaystyle{\sum_{n=1}^{\infty} }b_n\sin(\omega_nt)}_{\textrm{termes impaires}}\)

Remarquer que \(a_0\) est une "fonction constante" qui ne dépend pas de \(t\), donc garde le même valeur en \(t\) et en \(-t\) . La "fonction constante" est donc une fonction paire.

\(F\) paire \(\Leftrightarrow F(t)=a_0+\displaystyle{\sum_{n=1}^{\infty}}a_n\cos(\omega_nt)\)

\(G\) impaire \(\Leftrightarrow G(t)= \displaystyle{\sum_{n=1}^{\infty}}b_n\cos(\omega_nt)\)

3-

On considère la fonction \(F\) paire de période \(T\) définie par :

\(F(t)=a\) pour \(t \in [-\frac{T}{4} ;+ \frac{T} {4}]\)

\(F(t)=0\) pour \(t \in ]\frac{T}{4} ; 3 \frac{T}{4}[\)

\(\Rightarrow F(t)=a_0+\displaystyle{\sum_{n=1}^{\infty}}a_n\cos(\omega_nt)\) avec \(\omega_n=n ~\omega_1\) et \(\omega_1=\omega=\frac{2\pi}{T}\)

\(a_0=\frac{1}{T}\int^{(T)}F(t)dt=\frac{1}{T}\int_{-{T}/{4}}^{+{T}/{4}}a.dt=\frac{a}{2}\) valeur moyenne de la fonction \(F\) sur une période.

\(\omega_nT=n\omega_1T=2np\)

\(\Rightarrow a_n=\frac{2}{T}\int_{-{T} / {4}}^{+{T} / {4}}a.\cos(\omega_nt)dt=\frac{2}{T}\frac{a}{\omega_n} [\sin(\omega_nt)]_{-{T} / {4}}^{{T} / {4}}=\frac{a}{n\pi}[\sin n\frac{\pi}{2}-\sin(-n\frac{\pi}{2})]\)

Dans cette expression de \(a_n , n >0\) puisque le terme \(a_0\) a été sorti de la somme. \(\Rightarrow a_n=\frac{2a}{n\pi}\sin n\frac{\pi}{2}\)

\(n\) pair \(\Rightarrow \sin n\frac{\pi}{2}=0\Rightarrow a_n=0\)

\(n\) impair \(\Rightarrow n=2p+1\) (\(p\) entier) \(\Rightarrow \sin(2p+1)\frac{\pi}{2}=(-1)^p\)

\(\Rightarrow a_n=a_{2p+1}=\frac{2a}{(2p+1)\pi}(-1)^p\)

\(a_1=\frac{2a}{\pi} \Rightarrow\) pour \(n\) impair : \(n=2p+1 \Rightarrow \frac{a_n}{a_1}=\frac{1}{n}(-1)^p\)

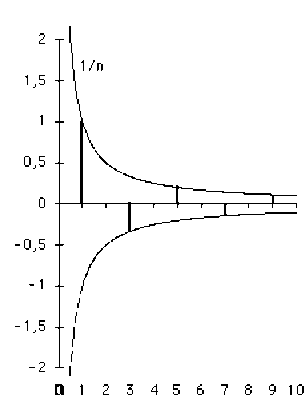
La série des \(a_n\) est alternée. En module : \(|a_n|=\frac{2a}{n\pi}\) et \(|\frac{a_n}{a_1}|=\frac{1}{n}\)

Les rapports \(\frac{a_n}{a_1}\) caractérisent la forme de la fonction périodique, quelle que soit son amplitude \(a\).

(Voir le spectre de Fourier de la fonction \(F\))

4-

On définit la fonction \(G\) impaire \([G(t)=-G(-t)]\) à partir de la fonction \(F\) impaire par une double translation d'origine :

  • translation selon l'axe \(t\) (translation horizontale), de \(\frac{T} {4}\) ou de \(- \frac {T} {4}\)

  • translation selon l'axe vertical, de \(- \frac{a}{2}\)

Alors : \(G(t)=\frac{a}{2}\) pour \(t\in[0 ;\frac{T}{2}] ~G(t) =-\frac{a}{2}\) pour \(t\in]\frac{T}{2} ;T[\)

de la fonction F² paire
de la fonction G² impaire

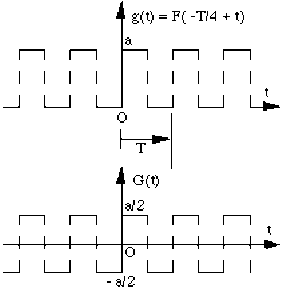
On a alors : \(g(t)=\frac{a}{2}+\displaystyle{\sum_{n=1}^{\infty}b_n\sin(\omega_nt)}\) qui est une fonction ni paire (à cause des sinus) ni impaire (à cause du terme constant \(\frac{a}{2}\))

et \(G(t)=\displaystyle{\sum_{n=1}^{\infty}b_n\sin(\omega_nt)}\) qui est une fonction impaire.

avec \(b_n=\frac{2}{T}\int^TG(t)\sin(\omega_nt)dt\Rightarrow b_n=\frac{2}{T}\frac{a}{2}[\int_0^{+{T}/{2}}\sin(\omega_nt)dt-\int_{-{T}/{2}}^T\sin(\omega_nt)dt]\)

\(=\frac{a}{T}(-\frac{1}{\omega_n})[\cos(-\frac{\omega_nt}{2})-\cos0-\cos\omega_nt+\cos\frac{\omega_nt}{2}]\)

\(\omega_nt=n\omega_1t=n2\pi\Rightarrow\cos\omega_n\frac{T}{2}=\cos n\pi=(-1)^n\Rightarrow b_n=+\frac{2a}{\omega_nT}[+1-(-1)^n]\)

\(n\) pair \(\Rightarrow (-1)^n=1\Rightarrow b_n=0\)

\(n\) impair \(\Rightarrow (-1)^n=-1 \Rightarrow b_n=+\frac{4a}{\omega_nT}\Rightarrow b_n=\frac{2a}{\pi}\frac{1}{n}\)

Remarquer que, pour \(n\) impair, les coefficients \(b_n\) sont toujours positifs et \(\frac{b_n}{b_1}=\frac{1}{n}\)

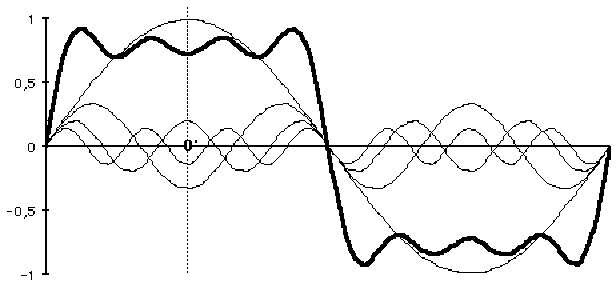
Sur ce schéma, le graphe en trait épais représente la somme des 7 premiers harmoniques non-nuls de la série de Fourier d'une fonction périodique carré symétrique.

  • Si on choisit l'origine \(O\) la fonction carré est impaire : tous les harmoniques sont des sinus dont la pente en \(O\) est positive, ils ont donc tous des coefficients d'amplitude \(b_n\) positifs.

  • Si on choisit l'origine en \(O'\) la fonction carré est paire : tous les harmoniques sont des cosinus dont l'amplitude \(a_n\) est alternativement positive et négative

Remarquer que \(\frac{b_n}{b_1}=\frac{1}{n}=\frac{|a_n|}{|a_1|}\).