Corde ayant une extrémité libre
Partie
Question
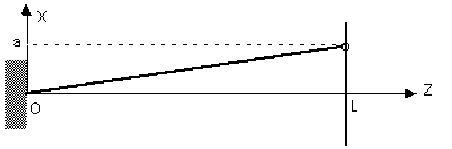
Une corde de longueur \(L\) est disposée sur un plan horizontal \((ZOX)\).
Au repos, elle est tendue selon la direction \(OZ\) et on notera \(T\) la norme de la force de tension.
Cette corde effectue des oscillations transversales de faible amplitude. Dans ce mouvement, elle glisse sans frottement sur le plan horizontal.
L'extrémité \(O\) de la corde reste fixe.
L'autre extrémité (en \(z=L\)) est fixée à un anneau (de masse négligeable) qui coulisse sans frottement sur une tige horizontale parallèle à \(OX\).
On notera \(\psi(z,t)\) la fonction représentant la vibration de la corde et on admettra que la condition précédente se traduit par le fait que, lorsque la corde oscille selon un mode propre, la valeur de la dérivée \(\left(\frac{\partial\psi}{\partial Z}\right)\) en \(z=L\) reste nulle à tout instant.
Compte tenu des conditions aux limites imposées à ce système, quel est l'ensemble des valeurs permises pour \(K\). La valeur de \(K\) dans le mode propre \(p\) sera notée \(K_p\).
En déduire l'expression \(\lambda_p\) des longueurs d'onde correspondantes.
Indiquer les valeurs \(K_1\) et \(\lambda_1\) pour le premier mode propre.
En déduire la valeur de la pulsation \(\omega_1\) du premier mode propre et celle \(\omega_p\) du mode \(p\).
En déduire l'expression la plus générale de la vibration dans ces conditions.
Conditions initiales imposées au système :
la vitesse initiale de chaque point de la corde est nulle,
la forme initiale de la corde est représentée par un segment dont l'extrémité mobile (en \(z=L\)) a une amplitude initiale : \(\psi(z=L, t=0)=a\).
Exprimer dans ces conditions la forme de la vibration \(\psi(z, t)\).
Rappel de cours
Voir la page Forme générale des modes propres
Solution détaillée
Remarque préliminaire : la condition \(\frac{\partial\psi}{\partial Z}= 0\) en \(Z=L\) signifie que la corde vibrante, dans un mode propre, a une tangente en \(z=L\) qui est parallèle à l'axe \(OZ\), et donc orthogonale au déplacement de l'anneau de fixation. L'anneau est donc soumis à une force de tension orthogonale à la direction \((OX)\) de son mouvement, et comme on suppose qu'il n'y a pas de frottement, celà signifie que la résultante des forces auxquelles est soumis l'anneau est orthogonale à son mouvement.
En lui appliquant le PFD en projection sur l'axe de son mouvement, on a donc : \(0 = m.\frac{d^2X}{dt^2}\) en appelant m la masse de l'anneau.
Or, l'accélération de l'anneau est non nulle. La relation précédente nécessite donc que sa masse m soit nulle (ou tout au moins négligeable par rapport à la masse de la corde).
1-
Conditions aux limites
L'expression générale d'un mode propre est :
\(\psi_p(z,t)=A_p(z)\cos(\omega_pt+\alpha_p)=(A_p\cos K_pz+B_p\sin K_pz)\cos(\omega_pt+\alpha_p) ~\forall p\)
En \(z=0\), les conditions aux limites imposent \(\forall p, \forall t\) : \(\psi_p(z=0,t)=0\)
\(\Rightarrow\) le facteur \(A_p(z)=(A_p\cos K_pz+B_p\sin K_pz)=0 \textrm{ en }z = 0 \Rightarrow A_p=0 ~\forall p\)
Le facteur d'amplitude est donc : \(A_p(z) = B_p\sin K_pz\)
En \(z=L\), la condition : \(\frac{\partial\psi_p(z,t)}{\partial z}=0\Rightarrow \frac{d\sin K_pz}{dz}=0\Rightarrow \cos K_pL=0\) \(\forall p\)
\(\Rightarrow K_pL=\frac{\pi}{2}+n\pi\Rightarrow K_p=\frac{\pi}{2L}(2n+1)=p\frac{\pi}{2L}\) avec \(p\) (impair)\(=2n+1\)
Remarque sur la numérotation :
Le fondamental correspondant à \(p=1\) (\(p\) : impair de \(1\) à \(\infty\)) ou à \(n=1\) (\(n\) : tous entiers successifs).
Pour le fondamental : \(K_1=\frac{\pi}{2L}=\frac{2\pi}{\lambda_1}\) avec \(\lambda_1=4L\) et \(\omega_1=K_1\sqrt{\frac{T}{p}}\)
Pour fixer les idées, on compare ci-dessous la forme de l'état initial de la corde de la question 3- et les modes propres successifs :

Remarque sur le prolongement périodique et sur la symétrie du problème :
La corde vibre (sans frottement) sur le plan horizontal \(\Rightarrow\) la solution doit être symétrique en \(OX\) (symétrie par rapport à l'axe \(OZ\)) \(\Rightarrow\) la valeur moyenne de la fonction de \(z\) qui représente la forme des modes propres doit être nulle si on la calcule sur une période \(\lambda=\lambda_1\).
\(\Rightarrow\) la valeur moyenne de la fonction de \(z\) qui représente le prolongement périodique de la forme de la corde, doit être nulle si on la calcule sur une période \(\lambda=\lambda_1\) (puisque ce prolongement est une combinaison linéaire des modes propres qui possèdent eux-mêmes cette propriété). Cette condition interdit par exemple la forme des prolongements (1) et (3). Le prolongement (2) a une valeur moyenne nulle sur une période \((2L)\). Mais il accepte des harmoniques \(p\) pairs (à cause de la discontinuité du prolongement en \(z=L\)) : la condition aux limites en \(z=L\) n'est donc pas satisfaite.
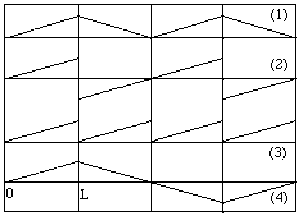
Le prolongement (4) satisfait à la fois les conditions aux limites et les conditions de symétrie.
Les schémas ci-dessus sont effectués en prenant pour forme initiale de la corde celle de la question 3- (pour fixer les idées) mais cette discussion ci-dessus est plus générale.
2-
Avec les conditions aux limites imposées ici :
Les modes propres sont de la forme :
\(\psi_p(z,t)=B_p\sin K_pz\cos(\omega_pt+\alpha_p)\), \(\forall p\) impairs et \(z \in [0,L]\)
L'expression générale de la vibration de cette corde est donc :
\(\psi(z,t)=\displaystyle{\sum_{p=1}^{p=\infty}B_p\sin K_pz\cos(\omega_pt+\alpha_p)}\) \(\forall p\) impairs et \(z \in [0,L]\)
Récapitulatif :
\(B_p\sin K_pz\) \(\forall p\) impairs et \(z \in[0,L]\) | forme du mode propre \(p\) de la corde. |
\(B_p\sin K_pz\) \(\forall p\) impairs et \(z \in[-\infty,+\infty]\) | terme \(p\) de la série de Fourier représentant le prolongement périodique de la forme de la corde. |
\(F(z)=\displaystyle{\sum_{p=1}^{p=\infty}B_p\sin K_pz}\), \(\forall p\) impairs et \(z \in[-\infty,+\infty]\) | série de Fourier représentant le prolongement périodique de la forme de la corde. |
\(\psi(z,t)=\displaystyle{\sum_{p=1}^{p=\infty}B_p\sin K_pz\cos(\omega_pt+a_p)}\), \(\forall p\) impairs et \(z \in[-\infty,+\infty]\) | vibration du prolongement périodique de la corde. |
La restriction sur \([0,L]\) de cette fonction \(\psi(z,t)\) représente la vibration de la corde : la théorie de Fourier (sous réserve d'effectuer le prolongement périodique adéquat) permet ainsi de calculer les coefficients du développement sur la base des modes propres.
3-
Pour utiliser les conditions initiales de vitesse imposées au système, il faut exprimer la vitesse en \(t=0\) :
\(\psi'(z,t=0)=\displaystyle{\sum_{p=1}^{p=\infty}-\omega_pB_p \sin K_pz \sin(\omega_p.0+\alpha_p)=0}\) \(\forall z\in[0,L]\), condition qui peut être satisfaite en choisissant \(\alpha_p=0, \forall p\).
La vibration de la corde s'exprime alors : \(\psi(z,t)=\displaystyle{\sum_{p=1}^{p=\infty}B_p\sin K_pz\cos(\omega_pt)}\), \(\forall p\) impairs et \(z\in[0,l]\)
Il suffit maintenant de calculer les coefficients de Fourier \(B_p\): les valeurs que nous trouverons pour ces coefficients caractériseront complètement la forme initiale de la corde et sa vibration.
Notons \(F\) la fonction de \(z \in[-\infty,+\infty]\) qui représente le prolongement périodique de la forme initiale de la corde avec \(\lambda_1=4L\) : \(B_p=\frac{2}{\lambda_1} \int^{(\lambda_1)}F(z)\sin K_pz.dz=\frac{1}{L}\int_{0}^{2L}F(z)\sin K_pz.dz ~\forall p\) impairs
(le produit : \(F(z)\sin K_pz\) étant une fonction paire).
\(F(z)=\frac{a}{L}z\) pour \(z \in[0,L]\) et \(F(z)=-\frac{a}{L}(z-2L)\) pour \(z \in[L,2L]\)
\(\Rightarrow B_p=\frac{a}{L^2}\int_0^L z .\sin K_p .z. dz-\frac{a}{L^2}\int_L^{2L}z\sin k_p . z . dz+\frac{2a}{L}\int_L^{2L}\sin K_p . z . dz\) \(\forall p\) impairs
On pose : \(\int\sin K_pz . dz=-\frac{1}{K_p}\cos(K_pz)=\mathcal P(z)\) avec \(p=(2n+1)\)
\(\int z\sin K_pz.dz=-\frac{z}{K_p}\cos(K_pz)+\frac{\sin(K_pz)}{(K_p)^2}=\mathcal I(z) \quad K_pL=\frac{\pi}{2}(2n+1)\)
\(\Rightarrow B_p=\frac{a}{L^2}[(\mathcal I(L)-\mathcal I(0))-(\mathcal I(2L)-\mathcal I(L))]+\frac{2a}{L}[\mathcal P(2L)-\mathcal P(L)]\)
avec : \(\mathcal P(L)=0\quad \mathcal P(2L)=+\frac{1}{K_p} \quad \mathcal I(0)=0 \quad \mathcal I(L)=\frac{\sin K_pL}{(K_p)^2}=\frac{(-1)^h}{K_p^2}\)
\(\cos(2K_pL)=\cos[\pi+(p-1)2\pi]=-1\Rightarrow \mathcal I(2L)=\frac{2L}{K_p}\)
\(\sin(2K_pL)=0\)
\(\Rightarrow B_p=\frac{8a(-1)^n}{\pi^2(2n+1)^2}\) avec \(p\) impair : \(p=2n+1\) \(\forall n\) entiers de \(0\) à \(+\infty\), avec : \(K_1=\frac{\pi}{2L}\) et \(K_p=pK_1=(2n+1)K_1\)
\(\omega_1=K_1\sqrt{\frac{T}{p}}\) et \(\omega_p=p\omega_1=(2n+1)\omega_1\)
la vibration de la corde s'exprime :
\(\psi(z,t)=\frac{8a}{\pi^2}\displaystyle{\sum_{n=0}^{n=\infty}\frac{(-1)^n}{(2n+1)^2} . \sin(2n+1).K_1 .z . \cos(2n+1).\omega_1 .t}\) \(~\forall n\) entiers de \(0\) à \(+\infty\).