Transformée de Fourier d'un double créneau

Partie

Question

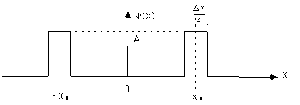
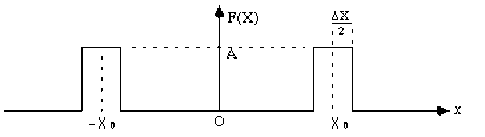
Soit \(\psi\) la fonction de variable \(X\) représentée par le graphe ci-contre.

Cette fonction est nulle partout, sauf sur les 2 créneaux [ de largeur \(\Delta X\) et centrés respectivement en \(X =+X_0\) et \(X=-X_0\) ] où cette fonction vaut \(A\).

  1. Déterminer (sur la base des exponentielles complexes) le spectre \(f(K)\) de cette fonction \(\psi\).

  2. Représenter \(|f(K)|\).

Rappel de cours

voir la page Exemple : impulsion temporelle en créneau

Solution détaillée

  1. Le spectre \(f(K)\) de la fonction \(F\) est : \(f(K)=\frac{1}{2\pi}\int_{-\infty}^{+\infty}F(x)e^{-iKx}dx=\frac{A}{2\pi}\int_{-X_0-\frac{\Delta X}{2}}^{-X_0+\frac{\Delta X}{2}}e^{-iKx}dx+\frac{A}{2\pi}\int_{+X_0-\frac{\Delta X}{2}}^{+X_0+\frac{\Delta X}{2}}e^{-iKx}dx\)

    \(=\frac{A}{2\pi(-iK)}[e^{-iK(-X_0+\frac{\Delta X}{2})}-e^{-iK(-X_0-\frac{\Delta X}{2})}+e^{-iK(X_0+\frac{\Delta X}{2})}-e^{-iK(X_0-\frac{\Delta X}{2})}]\)

    \(=\frac{A}{2\pi(-iK)}[e^{iKX_0}(e^{iK(\frac{\Delta X}{2})}-e^{-iK(\frac{\Delta X}{2})})+e^{-iKX_0}(e^{iK(\frac{\Delta X}{2})}-e^{-iK(\frac{\Delta X}{2})})]\)

    \(=2\frac{A}{\pi K}[\frac{e^{iK(\frac{\Delta X}{2})}-e^{-iK(\frac{\Delta X}{2})}}{2i}].[\frac{e^{iKX_0}-e^{-iKX_0}}{2}]\)

    \(=\frac{2A}{\pi K}\sin\frac{K\Delta X}{2}\cos KX_0\Rightarrow f(K)=\frac{A\Delta X}{\pi}\frac{\sin\frac{K\Delta X}{2}}{\frac{K\Delta X}{2}}\cos KX_0\)

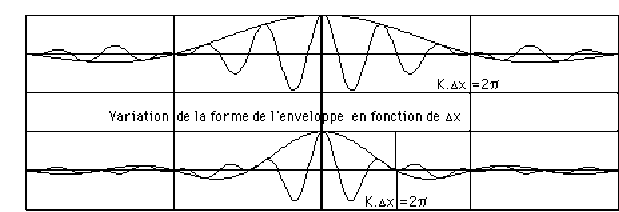
L'enveloppe de \(f(K)\) est la fonction : \(\frac{\sin u}{u}\) avec \(u=\frac{K\Delta x}{2}\)

Plus \(\Delta x\) est grand, plus l'enveloppe du spectre est resserrée.

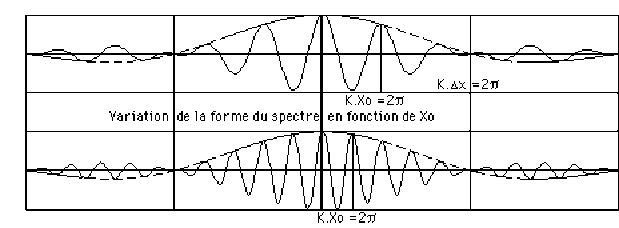
A l'intérieur de cette enveloppe, la variation d'amplitude en fonction de \(K\) est donnée par le facteur : \(\cos KX_0\) où \(X_0\) est la distance entre le centre des sources.

Plus la distance \(X_0\) est grande, plus le spectre est resserré.