Impulsions successives
Partie
Question
Une source émet deux impulsions successives identiques. L'amplitude de chacune d'elles est \(A = \textrm{constante}\) pendant une durée égale à \(2T\), la seconde impulsion démarre au bout d'un intervalle de temps égal à \(4T\) à près la fin de la première.
La première impulsion est centrée au temps \(t_1\) et la seconde au temps \(t_2\)
Exprimer cette fonction \(t \to F(t)\) pour \(t\in [-\infty,+\infty]\) et représenter son graphe.
A quel type de spectre peut-on s'attendre pour cette fonction, et comment peut-on l'interpréter en termes de diffraction et d'interférences ?
Ecrire l'expression générale permettant de déterminer le spectre d'une fonction non périodique, sur la base des exponentielles complexes.
En déduire le spectre \(f(\omega)\) de cette fonction \(\psi(t)\).
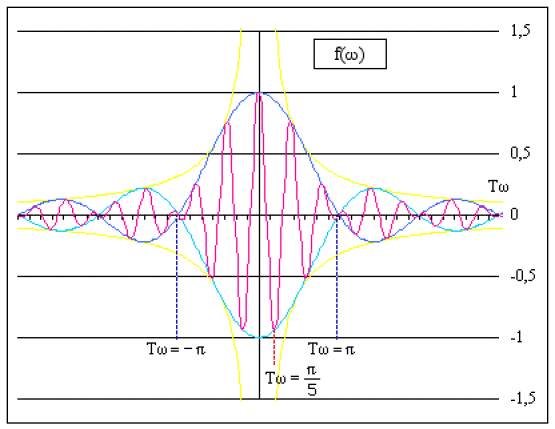
Représenter le module du spectre \(f(\omega)\).
Préciser la largeur \(\Delta\omega\) de la bande centrale.
Donner l'expression de l'onde progressive se propageant selon l'axe \(oz\) à partir d'une source (placée en \(z=0\)) dont la vibration est représentée par la fonction \(\psi(t)\) précédente.
Solution détaillée
1-
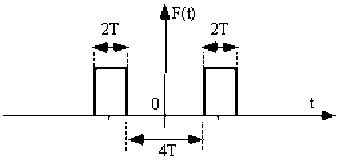
On a intérêt à choisir l'origine des temps de sorte que la fonction \(F\) soit paire (symétrique par rapport à \(0\))
* \(F(t) = A\) pour \(t \in [-6T , -4T] \cup [4T , 6T]\)
* \(F(t) = A\) pour \(t\) n'appartenant pas à cet intervalle.
2-
La largeur temporelle \((2T)\) \(\Rightarrow\) spectre en \((\omega)\) : \(\frac{sin \mu}{ \mu}\) (sorte de "diffraction temporelle")
La présence des \(2\) créneaux \(\Rightarrow\) sorte "d'interférences temporelles"
3-
\(f(\omega)=\frac{1}{2\pi}\int_{-\infty}^{+\infty}F(t)e^{+i\omega t}dt\Rightarrow 2 \pi f(\omega)=A\int_{-6T}^{-4T}e^{+i\omega t}dt+A\int_{6T}^{4T}e^{+i\omega t}dt\)
\(\frac{2\pi}{A}f(\omega)=\frac{1}{(-i\omega)}\left[e^{i\omega4T}-e^{+i\omega6T}+e^{-i\omega6T}-e^{-i\omega4T}\right]\)
\(=\frac{2}{\omega}\left[\frac{e^{i\omega6T}-e^{i\omega6T}}{2i}-\frac{e^{i\omega4T}-e^{-i\omega4T}}{2i}\right]\)
\(=\frac{2}{\omega}(\sin6\omega T-\sin4\omega T)\)
\(f(\omega)=\frac{A}{\pi\omega}(\sin6\omega T-\sin4\omega T)\)
\(\sin p-\sin q=2\sin\frac{p-q}{2}\cos\frac{p+q}{2}\Rightarrow \sin6\omega T-\sin4\omega T=2\sin\omega T . \cos5\omega T\)
Dans l'expression ci-dessous : \(T\) est une donnée, \(\omega\) est la variable
\(\Rightarrow f(\omega)=\frac{2A}{\pi\omega}\cos5\omega T\sin\omega T=\frac{2AT}{\pi}\cos(5T\omega)\frac{\sin(T\omega)}{(T\omega)}\)
4-
vibration de la source en \(z=0\) : \(\psi(0,t)=\int_{-\infty}^{+\infty}f(\omega)e^{i\omega t}d\omega\)
\(\Rightarrow \psi(0,t)=\frac{A}{\pi\omega}\left[\int_{-\infty}^{+\infty}\sin6T\omega . e^{+i\omega t}d\omega-\int_{-\infty}^{+\infty}\sin4T\omega . e^{+i\omega t}d\omega\right]\)
Vibration en \(z\neq0\) : \(\Rightarrow \psi(z,t)=\frac{A}{\pi\omega}\left[\int_{-\infty}^{+\infty}\sin6T\omega . e^{+i(\omega t-K(\omega)z)}d\omega-\int_{-\infty}^{+\infty}\sin4T\omega . e^{+i(\omega t-K(\omega)z)}d\omega\right]\)
Pas de dispersion (vitesse \(V\) la même \(\forall \omega\))\(\Rightarrow \omega t-K(\omega)z=\omega[t-\frac{K(\omega)}{\omega}z]=\omega(t-\frac{z}{V})\)
\(\psi(z,t)=\frac{A}{\pi\omega}\left(\int_{-\infty}^{+\infty}\sin6T\omega e^{+i\omega(t-\frac{z}{V})}d\omega-\int_{-\infty}^{+\infty}\sin4T\omega e^{+\omega(t-\frac{z}{V})}d\omega\right)\)
\(\psi(0,(t-\frac{z}{V}))\equiv\psi(z,t)\Leftarrow\) {obtenu en remplaçant \(t\) par \(t-\frac{z}{V}\) dans \(\psi(0,t)\)
\(\psi(0,t)\equiv\psi(z,t+\frac{z}{V})\)
Vibration en \(z=0\) à l'instant \(t\) \(\equiv\) vibration en \(z\) à l'instant ultérieur : \(t+\frac{z}{V}\)
\(\Delta t=\frac{z}{V}\) représentant le temps nécessaire pour que la vibration atteigne le point d'abscisse \(z\) (vitesse \(V\) \(\forall \omega\)). On retrouve donc par l'expression de la propagation de l'ensemble du spectre \(f(\omega)\) à la vitesse \(V\) que la forme \(\psi(0, z)\) de la vibration de la source se propage sans dispersion (sans "déformation") i.e simple translation de la vibration
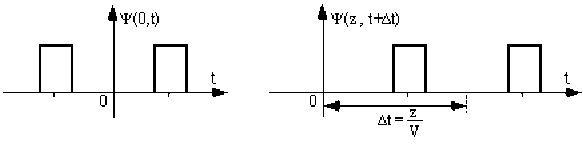
\(\Delta t\) plus tard que la source, le point d'abscisse \(z\) vibrera de la même façon que la source située en \(z=0\)
Spectre de la fonction \(\left \{\begin{array}{l} \psi(z,t)=A \textrm{ pour }t\in[t_1-6T,t_1-4T] \cup [t_1+4T, t_1+6T] \\ =0 \textrm{ en dehors} \end{array}\right.\)
\(f_z(\omega)=\frac{1}{2\pi}\int_{-\infty}^{+\infty}F(t)e^{i\omega t}dt\equiv\frac{1}{2\pi}\int_{-\infty}^{+\infty}\psi(z,t)e^{-i\omega t}dt\)
\(=\frac{A}{2\pi}\left[\int_{t_1-6T}^{t_1-4T}e^{i\omega t}dt+\int_{t_1+4T}^{t_1+6T}e^{-i\omega t}dt\right]\)
\(=\frac{Ae^{-i\omega t_1}}{2\pi(-i\omega)}(e^{i\omega4T}-e^{+i\omega6T}+e^{-i\omega6T}-e^{-i\omega4T})=\frac{Ae^{-i\omega t_1}}{\pi\omega}\left(\frac{e^{-i\omega6T}-e^{-i\omega6T}}{2i}-\frac{e^{i\omega4T}-e^{-i\omega4T}}{2i}\right)\)
\(=\frac{A}{\pi\omega}e^{-i\omega t_1}(\sin6T\omega-\sin4T\omega)=f_z(\omega)\) [spectre de la vibration à l'abscisse \(z=Vt_1\)]
Il s'agit donc de vérifier que \(f_z (\omega)\) est bien identique à l'expression du spectre déduit de \(\psi(z,t)\)
\(\psi(z,t)=\frac{A}{\pi\omega}\int_{-\infty}^{+\infty}f(\omega)e^{i\omega(t-\frac{z}{V})}=\frac{A}{\pi\omega}\int_{-\infty}^{+\infty}f(\omega)e^{-i\omega\frac{z}{V}}e^{i\omega t}d\omega\)
la densité spectrale en \(\omega\) à l'abscisse \(z\) est donc le produit de \(f(\omega)\) par le facteur \(e^{-i \omega \frac{z}{v}} \equiv e^{- i \omega t_{1}} \quad (t_{1} = \frac{z}{v} )\)
C'est bien la relation trouvée : \(f_z(\omega)=f(\omega) . e^{-i\omega t_1}\)