Transformée de Fourier d'un oscillateur amorti
Partie
Question
Rappeler l'expression générale du spectre de Fourier \(f(\omega)\) d'une fonction \(F(t)\) non périodique, sur la base des exponentielles complexes.
On considère le signal \(X(t)\) défini par : \(X(t)=0\) pour \(t \le 0\)
\(X(t)=X_0e^{-\lambda t}\sin\Omega t\) pour \(t>0\)
où \(\lambda\) et \(\Omega\) sont des coefficients réels, positifs, quelconques.
En utilisant l'expression de \(\sin\Omega t\) en fonction des exponentielles complexes, calculer l'intégrale représentant le spectre \(f(\omega)\) de la fonction \(X(t)\) définie ci-dessus. (le résultat sera une fonction de \(\omega\) dépendant aussi des paramètres du problème, à savoir : \(X_0\), \(\lambda\) et \(\Omega\)).
On pose : \(\Omega^2=\omega_0^2-\lambda^2\)
Donner la nouvelle expression de \(f(\omega)\) obtenue en éliminant le paramètre \(\Omega\).
En déduire \(|f(\omega)|=[f(\omega).\overline{f(\omega)}] ^{1/2}\)
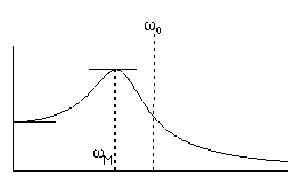
Déterminer la valeur de \(\omega\) qui rend la fonction \(|f(\omega)|\) maximum.
Déterminer le comportement de cette fonction : pour \(\omega\rightarrow 0\)
et en tracer le graphe pour \(\omega\rightarrow\infty\)
On considère un circuit série \((R,L,C)\) fermé, et on repère les différences de potentiel \(V(t)\) aux bornes du condensateur.
À l'instant pris comme origine des temps, on fait varier la tension par une impulsion, ce qui se traduit par : \(V(t=0)=0\) et \(\dot V(t=0)=\Omega\)
Montrer que l'oscillation de tension aux bornes de \(C\) est régie par une équation différentielle qui peut se mettre sous la forme :
\(\ddot V(t)+2\lambda\dot V(t)+\omega_0^2V(t)=0\)
dans laquelle on explicitera la valeur des paramètres \(\lambda\) et \(\omega_0\) en fonction des données \((R,L,C)\).
En admettant que, dans le cas où \(\lambda^2 < \omega_0^2\), la solution générale peut se mettre sous la forme : \(A.e^{-\lambda t} \cos (\Omega t + \varphi)\), exprimer la solution particulière satisfaisant les conditions initiales.
Dans ces conditions, que représente l'expression \(|f(\omega)|\) définie à la question \(c\).
Solution détaillée
1-
Expression générale du spectre de \(F\) : \(f(\omega)=\frac{1}{2\pi}\int_{-\infty}^{+\infty}F(t)e^{-j\omega t}dt\) avec \(j^2=-1\)
2-
En utilisant l'expression : \(\sin\Omega t=\frac{e^{j\Omega t}-e^{-j\Omega t}}{2j}\), le signal \(x(t)\) s'exprime :
\(\Rightarrow \left | \begin{array}{l} x(t)=0 \textrm{ pour }t \le 0 \\\\ x(t)=\frac{x_0}{2j}(e^{(-\lambda+j\Omega)t}-e^{(-\lambda-j\Omega)t}) \textrm{ pour }t > 0 \end{array}\right.\)
\(\Rightarrow f(\omega)=\frac{x_0}{4j\pi}\left\{\int_0^{+\infty}e^{(-\lambda+j(\Omega-\omega))t}dt-\int_0^{+\infty}e^{(-\lambda-j(\Omega+\omega))t}dt\right\}\)
\(=\frac{x_0}{4j\pi}\left(\frac{-1}{-\lambda+j(\Omega-\omega)}-\frac{-1}{-\lambda-j(\Omega-\omega)}\right)\)
\(=\frac{x_0}{4\pi}\left(\frac{1}{(\Omega-\omega) + j \lambda}+\frac{1}{(\Omega+\omega) - j \lambda}\right)\)
\(=\frac{x_0}{4\pi}\frac{(\Omega+\omega-j\lambda)+(\Omega-\omega)+j\lambda}{((\Omega-\omega)+j\lambda)((\Omega+\omega)-j\lambda)}\)
\(\Rightarrow f(\omega)=\frac{x_0}{2\pi}\frac{\Omega}{(\Omega^2-\omega^2+\lambda^2)+2j\lambda\omega}\)
3-
En posant : \(\omega_0^2=\Omega^2+\lambda^2\Rightarrow f(\omega)=\frac{x_0}{2\pi}\frac{\sqrt{\omega_0^2-\lambda^2}}{(\omega_0^2-\omega^2)+2\lambda j\omega}\)
\(\Rightarrow |f(\omega)|=\frac{x_0}{2\pi}\frac{\sqrt{\omega_0^2-\lambda^2}}{\sqrt{(\omega_0^2-\omega^2)^2+4\lambda^2\omega^2}}\)
Soit \(\omega_M\) la valeur de \(\omega\) qui rend \(f(\omega)\) Maximum (résonance), si ce Maximum existe.
Recherche du Maximum :
\((u^m)'=m ~u^{m-1}u'\Rightarrow |f(\omega)|'=\frac{x_0\sqrt{\omega_0^2-\lambda^2}}{2\pi}(-\frac{1}{2}) . u'^{-3/2}u'\)
avec \(u=(\omega_0^2-\omega^2)^2+4\lambda^2\omega^2\Rightarrow u'=2(\omega_0^2-\omega^2)(-2\omega)+8\lambda^2\omega\)
\(\Rightarrow u'=4\omega(\omega^2-\omega_0^2+2\lambda^2)\)
\(| f(\omega) | ' = - \frac{x_{0} \sqrt{\omega_{0}^{2} - \lambda^{2}}}{\pi} (( \omega_{0}^{2} - \omega^{2})^{2} + 4 \lambda^{2} \omega^{2}) ^{-3/2} . \omega. (\omega^{2} - \omega_{0}^{2} + 2 \lambda^{2})\)
\(\Rightarrow |f(\omega)|'=0\Leftrightarrow \left\{\begin{array}{l} \omega=0 \Leftarrow \textrm{ tangente horizontale (en }\omega=0) \textrm{ au graphe } \{ \omega, |f(\omega)| \}\\ \omega^2=\sqrt{\omega_0^2-\lambda^2} \Leftarrow \omega_M \textrm{ pulsation du Maximum de } |f(\omega)| ,\omega_M=\sqrt{\omega_0^2-\lambda^2} \end{array}\right.\)
en \(\omega=0\) : \(|f(\omega)|_{\omega=0}=\frac{x_0}{2\pi\omega_0}\sqrt{\omega_0^2-\lambda^2}\) (tangente horizontale)
\(|f(\omega)|_{\omega_M}=\frac{x_0}{2\pi}\frac{\sqrt{\omega_0^2-\lambda^2}}{\sqrt{(\omega_0^2-\omega^2_M)^2+4\lambda^2\omega_M^2}}\)
\(=\frac{x_0}{2\pi}\frac{\sqrt{\omega_0^2-\lambda^2}}{\sqrt{(\omega_0^2-\omega_0^2+2\lambda^2)^2+4\lambda^2(\omega_0^2-2\lambda^2)}}\)
\(=\frac{x_0}{2\pi}\frac{\sqrt{\omega_0^2-\lambda^2}}{\sqrt{4\lambda^2(\omega_0^2-2\lambda^2)}}=\frac{x_0}{4\pi\lambda}=|f(\omega)|_{\omega=\omega_M}\)
4-
Il est nécessaire de résonner algébriquement par rapport à un sens \(> 0\) de référence (choisi arbitrairement).
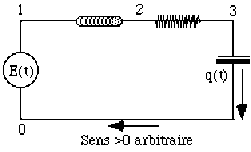
Conventions :
(1) on appelle f.e.m le ddp entre sortie et entrée (en référence au sens de parcours)
(2) la charge \(q\) du condensateur est celle portée par l'armature d'où sort la flèche correspondant au sens \(+\)
(1) On pose \(E(t) =V_1-V_0\) (noter qu'alors \(V_0\) pourra être le potentiel de référence , i.e. la masse)
La f.e.m d'induction est alors \(V_2-V_1 =-L\frac{di}{dt}\)
sens du courant \(\Rightarrow\) dans le sens \(+\Leftrightarrow i>0\)
les électrons vont dans le sens \(<0\)
\(\Rightarrow\) vont du générateur vers l'armature portant a charge \(q\) (côté borne \(0\))
\(\Rightarrow q(t)\downarrow \Rightarrow\frac{dq(t)}{dt}<0\)
\(i=-\frac{dq}{dt} \Rightarrow V_2-V_1 = +L\ddot q(t)\)
\(V_3-V_2=\) chute ohmique de tension dans la résistance \(\Leftrightarrow V_3<V_2\) si \(i>0\)
\(\Rightarrow V_3-V_2=-Ri=+R\dot q(t)\)
\(V_0-V_3=\frac{q(t)}{c}\) d'après la convention (2)
Dans la maille : \(E(t)=V_1-V_0=(V_1-V_2)+(V_2-V_3)+(V_3-V_0)\)
\(\Rightarrow E(t)=-L\ddot q-R\dot q-\frac{q}{C}\)
Pour obtenir l'équation définissant l'oscillation de tension aux bornes du condensateur, on a le choix : la tension \(V(t)\) peut désigner soit \(V_0-V_3\) , soit \(V_3-V_0\)
Cependant, il y a un argument physique à poser plutôt \(V(t)=V_3-V_0\) : le point \(O\) est alors potentiel de référence aussi bien pour \(e(t)\) que pour \(V(t)\). (Mais ce choix n'est pas obligatoire).
\(\Rightarrow\) On obtient dans ces conditions :
avec \(V(t)=V_3-V_0\) et \(E(t)=V_1-V_0 \Rightarrow E(t)=LC\ddot V+RC\dot V+V\)
et en posant : \(\omega_0^2=\frac{1}{LC}\) et \(\lambda=\frac{R}{2L}\) on obtient \(\omega_0^2E(t)=\ddot V(t)+2\lambda\dot V(t)+\omega_0^2V(t)\)
S' il n' y a pas de source \(\Rightarrow \ddot V(t)+2\lambda\dot V(t)+\omega_0^2V(t) = 0\)
Cela n'est évidemment pas nécessaire de passer par le cas où l'on a une source \(e(t)\) en série, mais cette mise en équation est à traiter de façon détaillée.
5-
Résolution de l'équation \(\ddot V(t)+2\lambda\dot V(t)+\omega_0^2V(t)=0\) dans le cas :\( \lambda^2<\omega_0^2\).
Discriminant de l'équation caractéristique : \(\alpha^2+2\lambda\alpha+\omega_0^2=0\)
\(\Delta'=\lambda^2+\omega_0^2<0\Rightarrow\) on pose \(\Omega^2=\omega_0^2-\lambda^2\) \((>0)\)
\(\Rightarrow\) solutions \(\alpha_1=-\lambda+j\Omega\) et \(\alpha_2=-\lambda-j\Omega\)
Remarquer que cette "technique" de résolution revient à chercher à exprimer les solutions de l'équation différentielle sur la base des exponentielles complexes : \(e^{\alpha t}\) avec \(\alpha\in C\)
alors : \(V=V_0e^{\alpha t}\Rightarrow\dot V=V_0\alpha e^{\alpha t}\Rightarrow\ddot V=V_0\alpha^2e^{\alpha t}\)
\(\Rightarrow V_0(\alpha^2+2\lambda+\omega_0^2)e^{\alpha t}=0 ~\forall t\)
\(\Rightarrow (\alpha^2+2\lambda+\omega_0^2)=0\)
La solution de l'équation différentielle est donc une combinaison linéaire des solutions :
\(V(t)=V_0e^{-\lambda t}(\alpha e^{j\Omega t}+\beta e^{-j\Omega t})\) avec \(\left(\begin {array} {c} \alpha_{1} \\ \alpha_{2} \end {array}\right)\)
Pour que cette solution soit réelle, il faut que dans cette somme l'un des termes soit le conjugué de l'autre (de sorte que la somme des parties imaginaires s'annule)
\(\Rightarrow \beta=\overline{\alpha}\) (complexe conjugué de \(\alpha\))
En posant : \(\alpha=\frac{e^{j\varphi}}{2}\) et \(\beta=\frac{e^{-j\varphi}}{2} \Rightarrow V(t)=V_0e^{-\lambda t}\left(\frac{e^{j(\Omega t+\varphi)}+e^{-j(\Omega t+\varphi)}}{2}\right)\)
\(V(t)=V_0e^{-\lambda t}\cos(\Omega t+\varphi)\)
Conditions initiales :
\(t=0 \Rightarrow V(0)=V_0\cos \varphi\)
\(\Rightarrow\) la condition initiale \(V(0)=0\) est satisfaite en posant \(\cos j=0\). On choisit\( \varphi=\frac{\pi}{2}\)
\(\Rightarrow V(t)=V_0e^{-\lambda t}\sin\Omega t\Rightarrow \dot V(t)=V_0(e^{-\lambda t}\sin\Omega t)'\)
\(\dot V(t)=-\lambda V_0 e^{-\lambda t}\sin\Omega t+\Omega V_0 e^{-\lambda t}\cos\Omega t\)
\(\dot V(t)_{t=0}=0+\Omega V_0\)
(condition initiale fixée)
Le circuit considéré (voir schéma précédent) dans le cas \((\lambda^2<\omega_0^2)\) est résonnant (\(\lambda=\frac{R}{2L}\) et \(\omega_0^2=\frac{1}{LC}\))
Admettons qu'on puisse disposer d'une source \(E(t)\) qui crée les conditions initiales fixées \(\Rightarrow V(t)\)
\(f(\omega)\) (calculée en -2) est alors le spectre de Fourier de la tension \(V(t)\) aux bornes du condensateur : \(V(\omega)=\frac{V_0}{2\pi}\frac{\sqrt{\omega_0^2-\lambda^2}}{\sqrt{(\omega_0^2-\omega^2)}+2\lambda j\omega}\)
On montrera en TP que si on excite le circuit avec une source \(E(t)\) périodique de tension carrée, alors, le circuit est excité par ce carré périodique, i.e. par l'ensemble des harmoniques (aux différentes pulsations \(\omega_n = n \omega_1\), \(\forall n\) ,de ce carré).
Alors : \(V(\omega_n)=\frac{V_0}{2\pi}\frac{\sqrt{\omega_0^2-\lambda^2}}{\sqrt{(\omega_0^2-\omega_n^2)}+2\lambda j\omega_n}\Rightarrow |V(\omega_n)|=\frac{V_0}{2\pi}\frac{\sqrt{\omega_0^2-\lambda^2}}{\sqrt{(\omega_0^2-\omega_n^2)}+4\lambda^2\omega_n^2}\)
En appelant \(e(\omega_n)\) l'amplitude de la composante de pulsation \(\omega_n\) de la source i.e \(|e(\omega_n)|=e_n\Rightarrow\frac{V(\omega_n)}{e(\omega_n)}=y_n\) (facteur de surtension à la pulsation \(\omega_n\))
L'ensemble des valeurs des pulsations \((\forall n)\) permet de tracer la courbe de résonance du circuit (obtenue point par point, aux valeurs \(\omega_n= n.\omega_1\)).