Relation d'incertitude (1)
Partie
Question
Soit \(f(\omega)\) le spectre (sur la base des exponentielles complexes) d'une fonction \(\psi\) non périodique de variable \(t\), défini par :
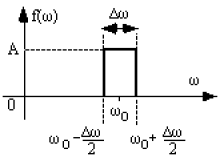
\(f(\omega)=A\) pour \(\omega\in [\frac{\omega_0-\Delta\omega}{2} ,\frac{\omega_0+\Delta\omega}{2}]\), où \(\Delta\omega\) est quelconque
\(f(\omega)=0\) en dehors de cet intervalle.
Déterminer la fonction \(\psi(t)\) dont \(f(\omega)\) est le spectre.
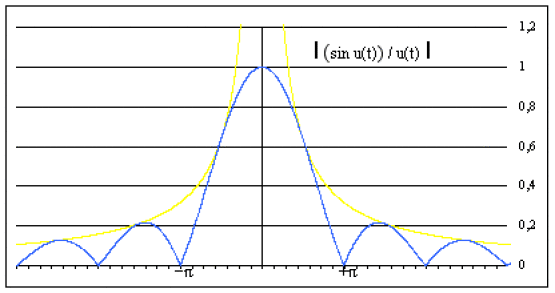
Représenter \(|\psi(t)|\)
En appelant \(\Delta t\) la durée (entre \(2\) valeurs nulles de \(\psi\)) pendant laquelle la vibration \(\psi(t)\) présente une amplitude la plus importante, montrer la relation \(\Delta t.\Delta\omega =4\pi\).
Solution détaillée
Rappel :
\(F(t)=\int_{-\infty}^{+\infty}f(\omega)e^{i\omega t}d\omega\) et \(f(\omega)=\frac{1}{2\pi}=\int_{-\infty}^{+\infty}F(t)e^{-i\omega t}dt\)
1-
\(\psi(t)=A\int_{\omega_0-\frac{\Delta\omega}{2}}^{\omega_0+\frac{\Delta\omega}{2}}e^{i\omega t}d\omega=\frac{A}{it}e^{i\omega_0t}(e^{i\frac{\Delta\omega}{2}t}-e^{-i\frac{\Delta\omega}{2}t})\Rightarrow \psi(t)=\frac{2A}{t}e^{i\omega_0t}\sin\frac{\Delta\omega}{2}t\)
La fonction \(\psi\) est réelle si et seulement si \(\omega_0= 0\Leftrightarrow f(\omega)\) paire
2-
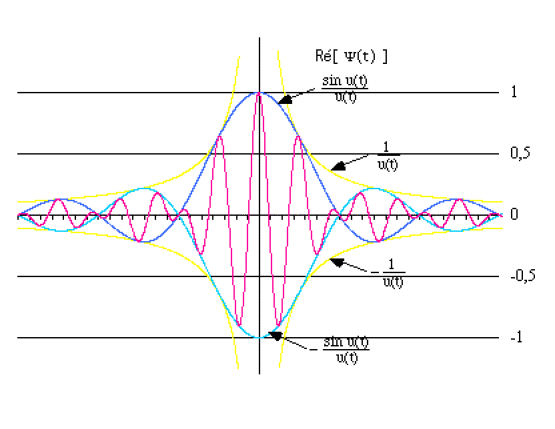
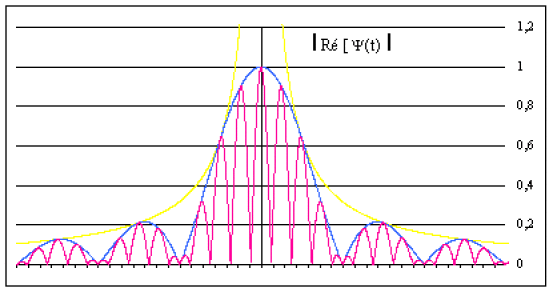
\(\psi(t)=e^{i\omega_0t} . A . \Delta\omega\frac{\sin\frac{\Delta\omega}{2}t}{\frac{\Delta\omega}{2}t}\Rightarrow \Re [\psi(t)]=A . \Delta\omega\frac{\sin\frac{\Delta\omega}{2}t}{\frac{\Delta\omega}{2}t} . \cos(\omega_0t)\)
et \(|\psi(t)|=A . \Delta\omega\left|\frac{\sin u(t)}{u(t)}\right|\) avec \(u(t)=\frac{\Delta\omega}{2}t\)
Les enveloppes en \((\sin u/u)\) et \((-\sin u/u)\) sont représentées ci-dessus, elles-mêmes limitées par les enveloppes en \((1/u)\) et \((-1/u)\).
3-
Les valeurs \(+\pi\) et \(-\pi\)
sont les premières qui annulent les sinus. \(\frac{\Delta\omega}{2} . \Delta t=2\pi\Leftrightarrow \Delta\omega . \Delta t=4\pi\)