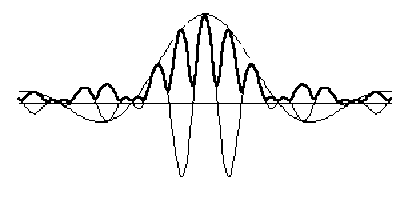
Propagation et interférence entre 2 sources
Partie
Question
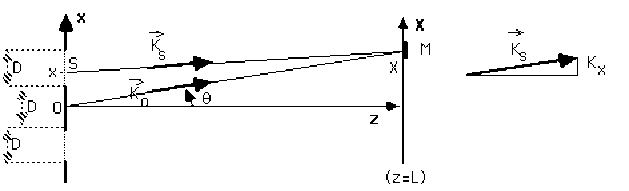
On considère \(2\) fentes parallèles identiques, de largeur \(D\) et séparées par la distance \(D\), situées dans le plan \(z=0\), et toutes deux parallèles à l'axe \(Oy\) .
Sur ces deux fentes arrive depuis la région \(z<0\) une onde plane, scalaire, monochromatique, de pulsation \(\omega\) et de vecteur d'onde dirigé dans le sens positif défini par \(Oz\). On appellera A l'amplitude de cette onde.
L'ensemble de ces deux fentes constitue ainsi une source de vibrations dont on se propose d'étudier la propagation dans le plan \((xOz)\) et dans la région \(z>0\).
1- Exprimer la densité d'amplitude \(F(x)\) de la vibration émise en fonction de l'abscisse \(x\) d'un point \(S\) quelconque appartenant au plan \(z=0\) de la source et représenter \(F(x)\) .
Exprimer la densité d'amplitude \(\psi_s(M, t)\) de la vibration qui arrive en un point \(M\) du plan \((z=L)\) qui a été émise par un point quelconque \(S\) du plan \((z=0)\), en fonction :
du facteur \(F(x)\) défini précédemment, relatif au point \(S\) considéré,
du vecteur \(\overrightarrow{SM}\) et du vecteur d'onde correspondant \(\overrightarrow{K_s}\)
de la pulsation \(\omega\).
En déduire l'amplitude élémentaire \(\delta\psi_s(M, t)\) de la densité de vibration arrivant au point \(M\), émise par une élément de source (de "largeur" \(dx\)) centré au point \(S\) .
2- On note \(\overrightarrow{K_0}\) le vecteur obtenu par projection (sur \(\overrightarrow{OM}\)) du vecteur d'onde \(\overrightarrow{K_s}\) (ce vecteur \(\overrightarrow{K_0}\) ne dépend donc pas de l'abscisse \(x\) du point \(S\)) et \(K_x\) la composante sur l'axe \(Ox\) du vecteur d'onde \(\overrightarrow{K_s}\).
Partant de la relation \(\overrightarrow{SM}=\overrightarrow{SO} +\overrightarrow{OM}\), exprimer le produit \(\overrightarrow{K_s}.\overrightarrow{SM}\) en fonction de \(K_x\), de \(x\), de \(\overrightarrow{OM}\) et de\( K_0\)
En déduire une expression de l'amplitude élémentaire \(\delta\psi_s(M, t)\) sous la forme d'un produit de facteurs que l'on interprètera comme traduisant:
un phénomène de propagation selon la direction \(\overrightarrow{OM}\)
la densité \(F(x)\)
le déphasage lié à la position x de l'élément de source centré en \(S\)
la "largeur" \(dx\) de l'élément.
3- En déduire l'expression de la densité de vibration \(\psi(M,t)\) en un point \(M\) produite par la totalité de la source.
Sachant que la transformée de Fourier d'une fonction paire est une fonction paire, mettre en évidence (dans l'expression précédente) un facteur \(f(K_x)\) représentant la transformée de Fourier de \(F(x)\).
Calculer et exprimer \(f(K_x)\) en fonction de \(K_x\), de \(A\) et de \(D\) .
Vérifier que le module de la densité de vibration \(\psi(M,t)\) au point \(M\) est donné par \(|f(K_x)|\)
Expliciter ce module par une fonction (que l'on notera \(G\)) telle que \(G(X) = | f(K_x) |\)
Représenter l'allure générale de \(G(X)\).
4- On dispose, centré au point \(M\) d'abscisse \(X\), un appareil de mesure qui possède une certaine largeur \(U\) et qui est sensible au module de la vibration .
Cet appareil détecte non pas directement le module de l'amplitude de la vibration s'étant propagé selon une direction \(\theta\) définie par la direction de \(OM\), mais il somme ces modules pour les vibrations s'étant propagé dans un domaine \(\Delta \theta\) (autour de la valeur \(\theta\)) défini par la largeur \(U\) de l'appareil de mesure.
On notera :
\(X\) l'abscisse centrale de l'appareil de mesure,
\(u\) l'abscisse d'un point de l'appareil, \(u \in\left[\frac{X-U}{2},\frac{X+U}{2}\right]\) et
\(S(u)\) sa sensibilité en fonction de la position \(u\) du point considéré.
Exprimer le résultat de cette mesure.
Dans le cas particulier où la sensibilité de cet appareil de mesure est supposée constante sur toute sa largeur \(U\), représenter schématiquement la mesure effectuée sur la grandeur à mesurer \(G(X)\) (par cet appareil centré à l'abscisse \(X\) ).
Déduire de la forme précédente l'expression de cette mesure.
Exprimer le résultat de la mesure dans le cas particulier où, de plus, l'appareil est centré sur une position pour laquelle \(G(X)\) est extrémum et où la largeur \(U\) de l'appareil est assez petite pour pouvoir considérer que \(G(X)\) varie peu sur le domaine \(U\).
Solution détaillée
1-
Soit \(F(x)\) la densité d'amplitude de la source (plan \(z=0\))
\(F(x)=0\) dans ce plan sauf sur les \(2\) fentes qui représentent la source.
\(F(x)=A\) sur les fentes, i.e. \(x\in \left[ -\frac{d}{2} -\frac{D}{2} , -\frac{d}{2} +\frac{D}{2} \right] \cup \left[\frac{d}{2} -\frac{D}{2} ,\frac{d}{2} +\frac{D}{2}\right]\)
Les \(2\) fentes émettrices de ce plan \((z=0)\) sont décrites alors par la fonction : \(F(x). e^{i\omega t}\)
Soit \(S\) un point de la source et \(M\) un point \(\in\) plan \((z=L)\)
\(\psi_s (M,t) = F(x).e^{i(\omega t-\overrightarrow{K_s}.\overrightarrow{SM})}\) densité d'amplitude en \(M\)
\(\delta\psi_s (M,t) = F(x).e^{i(\omega t-\overrightarrow{K_s} .\overrightarrow{SM})}\delta x\) amplitude élémentaire de la tranche "\(\delta x\)" située en \(M\)
Remarque : ce \(\delta\psi_s\) ne représente pas la différentielle de la fonction \(\psi_s (M,t)\) ci-dessus considérée comme fonction de \(M \left|\begin{array}{c} X \\ Y \\ Z \end{array}\right|\) et \(t\).
Le passage de la densité d'amplitude à l'amplitude élémentaire suppose que cette dernière est proportionnelle à la densité et à la largeur de source \(\delta x\) contribuant à l'amplitude élémentaire.
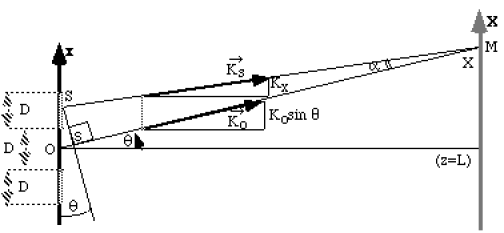
2-
\(-\overrightarrow{K_s}.\overrightarrow{SM}\simeq-\overrightarrow{K_0}.\overrightarrow{SM}=-\overrightarrow{K_0}.\overrightarrow{sO}-\overrightarrow{K_0}.\overrightarrow{OM} = \overrightarrow{K_0}.\overrightarrow{Os}-\overrightarrow{K_0}.\overrightarrow{OM}\Rightarrow e^{i(\omega t-\overrightarrow{K_s}.\overrightarrow{SM})} = e^{i(\omega t+\overrightarrow{K_0}.\overrightarrow{Os}-\overrightarrow{K_0}.\overrightarrow{OM})}\)
L'angle \(\alpha\) est très petit (voir le schéma ci-dessus) si \(M\) est assez loin de la source \(\Rightarrow K_x \simeq K_0 \sin \theta\)
On pose : \(OS=x\)
\(Os=x\sin \theta\Rightarrow \overrightarrow{K_0}.\overrightarrow{Os}=K_0.Os=-\frac{k_x}{\sin\theta}.x.\sin\theta=K_x.x\)
\(\Rightarrow e^{i(\omega t-\overrightarrow{K_s}.\overrightarrow{SM})}=e^{iK_xx}e^{i(\omega t-\overrightarrow{K_0}.\overrightarrow{OM})}\)
\(\Rightarrow \delta\psi_s(M,t)=\underbrace{F(x)}_{\textrm{densité}}\underbrace{e^{iK_xx}}_{\textrm{déphasage selon S}}\underbrace{e^{i(\omega t-\overrightarrow{K_0}.\overrightarrow{OM})}\delta x}_{\textrm{facteur de propagation selon la direction moyenne}\overrightarrow{OM}}\)
3-
Pour avoir la densité \(\psi\) produite par toute la source, il faut sommer \(\delta\psi_s(M_1,t)\) pour tous les points du plan émetteur, i.e \(\forall x\).
Comme le facteur de propagation ne dépend pas de la variable \(x\), on a : \(\psi(M,t)=\left[\int_{-\infty}^{+\infty}F(x).e^{iK_xx}dx\right].e^{i(\omega t-\overrightarrow{K_0}.\overrightarrow{OM})}\)
la transformée de Fourier de de \(F(x)\) est \(f(K_x)=\frac{1}{2\pi}\int_{-\infty}^{+\infty}F(x)e^{-iK_xx}dx\)
\(\Rightarrow f(-K_x)=\frac{1}{2\pi}\int_{-\infty}^{+\infty}F(x)e^{+iK_xx}dx\)
Mais sachant que \(F(x)\) est paire\(\Rightarrow f(K_x)\) paire, on a : \(\psi(M,t)=2\pi f(K_x)e^{i(\omega t-\overrightarrow{K_0}.\overrightarrow{OM})}\)
Le calcul de \(f(K_x)\) donne : \(f(K_x)=\frac{A}{2\pi}\left(\int_{-{dt}/{2}-{D t}/{2}}^{-{dt}/{2}+{Dt}/{2}}e^{-iK_xx}dx+\int_{{dt}/{2}-{D t}/{2}}^{{dt}/{2}+{Dt}/{2}}e^{-iK_xx}dx\right)\)
\(f(K_x)=\frac{2A}{\pi K_x}\sin K_x\frac{D}{2}.\cos K_x\frac{d}{2}\)
que l'on peut exprimer en faisant apparaître la fonction \(\frac{\sin u}{u}\)
\(f(K_x)=\frac{AD}{\pi}\frac{\sin(K_x\frac{D}{2})}{K_x\frac{D}{2}}.\cos(K_x\frac{d}{2})\)
Utilisant à nouveau : \(K_{x} \simeq K_{0} \sin \theta \Rightarrow f(K_{x}) = \frac{AD}{\pi} . \frac{\sin \frac{K_{0} D \sin \theta }{2}}{\frac{ K_{0} D \sin \theta }{2}} . \cos (K_{0} \frac{d}{2} \sin \theta )\)
\(\Rightarrow\) la densité de vibration en \((M_1,t)\) a pour module :
\(|\psi(M,t)|=2\pi|f(K_x)|.\underbrace {|e^{i(\omega t-\overrightarrow{K_0}.\overrightarrow{OM})}|} _{ \textrm{module} = 1 }\equiv \underbrace {2\pi|f(K_x)|}_{G(x)}\)
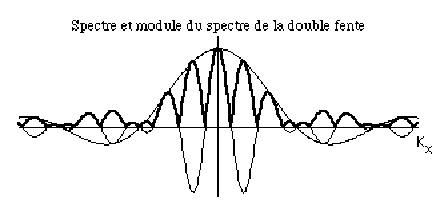
4-
Posons \(|\psi(M,t)|=G(x)\) la densité d'amplitude en module, avec \(G(x) = 2\pi|f(K_x)|\)
Supposons que l'on ait placé au point \(M\) un récepteur de largeur \(U\), centré en \(X\), dans le plan \((z=L)\) comme le représente le schéma précédent.
\(f\) la mesure par le récepteur en \(M\) est effectuée entre ( \(X -\frac{U}{2}\) et \(X +\frac{U}{2}\))
Sur la largeur du récepteur, l'angle \(\theta\) varie alors de \(\Delta \theta\).
En notant \(S(u)\) la sensibilité de l'appareil de mesure en fonction de la position \(u\) du point sur l'appareil, l'amplitude élémentaire de la mesure peut se représenter par :
\(S(u).|\psi(u,t)|\).du, et le résultat de la mesure en "\(X\)" est alors :
\(M(X,t)=\int_{X-\frac{U}{2}}^{X+\frac{U}{2}}S(u).|\psi(u,t)|.du=\frac{1}{2\pi}\int_{X-\frac{U}{2}}^{X+\frac{U}{2}}S(u).G(u)du\) (mesure en "\(X\)")
En particulier, si la sensibilité \(S(u)\) de l'appareil de mesure est constante (et notée \(S\)) sur l'intervalle \(\Delta \theta\) qui représente l'appareil de mesure, alors :
\(\Rightarrow M(X)=\frac{S}{2\pi}\int_{X-\frac{U}{2}}^{X+\frac{U}{2}}G(u)du\) où \(\int_{X-\frac{U}{2}}^{X+\frac{U}{2}}G(u)du\) est la valeur moyenne de \(G\) sur cet intervalle (courbe en gras).