Paquet d'onde
Partie
Question
On considère le paquet d'onde représenté par la superposition continue d'ondes monochromatiques, dont la densité d'amplitude en fonction de \(K\) est donnée par : \(f(K)=A\frac{e^{-(k-K_0)^2}}{2\beta^2}\)
où \(K\) est le module du vecteur d'onde : \(K =\frac{2\pi}{\lambda}\)
\(K_0\) est la valeur centrale du spectre et \(\beta\) est une constante réelle : \(\beta \ll K_0\)
Tracer le graphe de \(f(K)\)
Exprimer la vibration résultante comme partie réelle d'une fonction, \(\psi(0, t)\) à valeurs complexes.
En déduire l'expression générale \(\psi(x,t)\) représentant la propagation de cette vibration.
On admettra l'expression du développement en série de Taylor d'une fonction autour d'une valeur particulière de la variable, et on l'appliquera à la fonction \(\omega(K)\), à savoir :
\(\omega(K)=\omega(K_0)+(K-K_0)\left[\frac{d\omega}{dK}\right]_{K=K_0}+...+\frac{(K-K_0)^n}{n !}[\omega^{(n)}(K)]_{K=K_0}+...\)
Justifier le fait que l'on puisse ici limiter ce développement au premier ou au second ordre en \((K- K_0)\).
On effectuera dès lors le changement de variable : \(k = K - K_0\).
Dans un premier temps (questions: 4-5-6 et 7) on limitera ce développement au premier ordre,
puis au second ordre (question 8 et 9).
Exprimer \(\omega(K)\) en fonction de \(\omega_0 = \omega(K_0)\) et de la vitesse de groupe \(V_g\).
Montrer que \(\psi(x, t)\) peut s'exprimer sous la forme : \(\psi(x,t)=B(x,t)e^{i(\omega_0t-K_0)}\)
avec : \(B(x,t)=\int_{-\infty}^{+\infty}Ae^{-(\frac{k^2}{2\beta^2})}e^{ik(V_g.t-x)}dk\)
En admettant le résultat suivant : \(\int_{-\infty}^{+\infty}e^{-\alpha^2}d\alpha=\sqrt{\pi}\), en déduire l'expression de \(B(x, t)\) ainsi que celle de \(\psi(x,t)\).
Montrer que l'onde résultant est sinusoïdale modulée.
Déterminer la forme de la modulation, son maximum.
Montrer que le paquet d'onde se déplace sans se déformer à la vitesse \(V_g\).
Représenter le paquet d'onde en un point \(x_0\) : \(\psi(x_0, t)\) puis à l'instant \(t_0\) : \(\psi(x, t_0)\)
Dans cette dernière expression, calculer les abscisses \(x_1\) et \(x_2\) telles que les amplitudes de la modulation soient divisées par la valeur : \(e\).
Déduire la valeur des produits : \((x_2 -x_1).(K_2 - K_1)\) et \((\omega_2 - \omega_1).(t_2 - t_1)\)
En effectuant maintenant le développement jusqu'au second ordre et en posant :
\(k=K-K_0, ~ a=\left(\frac{d^2\omega}{d^2K}\right)_{(\textrm{en }K_0)}\) et \(f(t)=\left(\frac{1}{2\beta^2}\right)-i . \alpha . t\)
montrer que : \(\psi(x,t)=B(x,t).\cos(K_0x-\omega_0t)\)
Calculer \(B(x, t)\) et en déduire que le groupe d'onde se propage en se déformant.
Solution détaillée
1-
\(f(k)\) est symétrique par rapport à \(k = k_0\)
On note \(k_1\) et \(k_2\) les valeurs de \(k\) telles que :
\(A(k_1)=A(k_2)=A_0e^{-\frac{(k_1-k_0)^2}{2\beta^2}}=A_0e^{-\frac{(k_2-k_0)^2}{2\beta^2}}=\frac{A_0}{e}\)
\(\Rightarrow(k_1-k_0)^2=(k_2-k_0)^2=2\beta^2 \Rightarrow k_2-k_1=2(k_2-k_0)=\beta \sqrt2<<\sqrt2k_0\)
\(\Rightarrow \Delta k=\beta \sqrt2\)
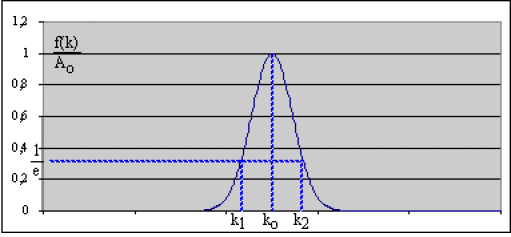
\(\beta <<k_0\Rightarrow\Delta k<<2\sqrt2k_0\) ou \(\frac{\Delta k}{k_0}<<2\sqrt2\)
2-
L'amplitude en fonction de \(k\) est : \(A(k)=A_0e^{-\frac{(k-k_0)^2}{2\beta^2}}\) \((\forall k)\)
\(\Rightarrow A(k)\) représente \((\forall k)\) l'amplitude de l'onde harmonique : \(A(k)\cos(\omega(k).t-kx)\)
\(\Rightarrow\) L'onde incidente : \(\psi(x,t)=\int_{-\infty}^{+\infty}A_0.e^{-\frac{(k-k_0)^2}{2\beta^2}}.\cos(\omega(k).t-k.x)dk\)
C'est la partie réelle de : \(\psi(x,t)=A_0\int_{-\infty}^{+\infty}A_0.e^{-\frac{(k-k_0)^2}{2\beta^2}}e^{i(\omega(k).t-k.x)}dk\)
3-
On effectue un développement en série de \(\omega(k) : \omega(k)=\omega(k_0)+(k-k_0)\left(\frac{d\omega}{dk}\right)_{k_0}+\left(\frac{(k-k_0)^2}{2}\right)\left(\frac{d^2\omega}{dk^2}\right)_{k_0}+\varepsilon(k-k_0)^3\)
on a vu que : \(k-k_0 \ll \sqrt2 ~ K_0\Leftarrow\) représente l'intervalle sur lequel \(A(k)\) a une valeur appréciable
\(\Rightarrow\) on limitera le développement :
soit au 1er ordre (questions 4..7)
soit au 2ème ordre (questions 8 et 9)
4-
On pose : \(\omega(k_0)=\omega_0\) et \(\left(\frac{d\omega}{dk}\right)_{k_0}=V_g=\)vitesse de groupe
\(\Rightarrow\) au 1er ordre : \(\omega(k)\simeq\omega_0+\Delta k\left(\frac{d\omega}{dk}\right)_{k_0}\)
\(\omega(k)\simeq\omega_0+(k-k_0)V_g=\omega_0+k'V_g\)
\(\Rightarrow \psi(x,t)=A_0\int_{-\infty}^{\infty}e^{-\frac{k'^2}{2\beta^2}}e^{i(\omega_0 t+k'V_g.t-kx)}dk'\)
On remplace : \(\omega_0t-kx=\omega_0t-k_0x+(k_0-k)x=(\omega_0t-k_0x)-k'x\)
\(\Rightarrow \begin{array}{l} \psi(x,t)=B(t)e^{i(\omega_0t-k_0x)} \\ B(t)=A_0\int_{-\infty}^{+\infty}e^{-\frac{k'^2}{2\beta^2}}e^{+ik'(V_g.t-x)}dk'\end{array}\)
5-
\(-\frac{k'^2}{2\beta^2}+ik'(V_g.t-x)=-\left(\frac{k'}{\sqrt2\beta}-i\frac{\sqrt2\beta}{2}(V_g.t-x)\right)^2-\frac{\beta^2}{2}(V_g.t-x)^2\)
on pose donc : \(l=\frac{k'}{\sqrt2\beta}-i\frac{\sqrt2\beta}{2}(V_g.t-x)\Rightarrow dk'=\beta . \sqrt2 . dl\)
\(\Rightarrow B(t)=A_0 . \sqrt2 . \beta . e^{-\frac{\beta^2}{2}(V_g.t-x)^2}\int_{-\infty}^{+\infty}e^{-l^2}dl\)
\(B(t)=A_0 . \sqrt{2 \pi} . \beta . e^{-\frac{\beta^2}{2}(V_g.t-x)^2}\Rightarrow \psi(x,t)\)
6-
On pose : \(\varphi(x,t)=\)partie réelle de \(\psi(x,t)\)
\(\varphi(x,t)=A ~\sqrt{2\pi} . \beta . e^{-\frac{\beta^2}{2}(V_g.t-x)^2}\cos(\omega_0t-k_0x)\)
La propagation du groupe d'onde (l'enveloppe de modulation) se fait à la vitesse \(V_g\) (appelée vitesse de groupe), vitesse qui est relative au facteur de modulation \(e^{-\frac{\beta^2}{2}(V_g.t-x)^2}.\)
À l'intérieur de cette enveloppe, la propagation de l'oscillation se fait à la vitesse \(V_0=-\frac{\omega_0}{k_0}\)
mais \(\omega=\omega_0+V_g(k-k_0)\Rightarrow V_g=\left(\frac{\omega-\omega_0}{k-k_0}\right)\) revient à dire que \(\omega\) varie linéairement avec \(k\) (si \(k\) est proche de \(k_0\)).
\(\Rightarrow\) le paquet se déplace sans déformation (mais on aura en général \(V_0\neq V_g\))
7-
\(\beta ~A~ \sqrt{2\pi} . e^{-\frac{\beta^2}{2}(V_g.t-x)^2}=\beta ~A~\sqrt{2\pi} . e^{-1}\Leftrightarrow\beta^2(V_g.t-x_1)^2=2\Leftrightarrow(V_g.t-x_1)^2=\frac{2}{\beta^2}\)
\(V_g.t-x_1=\frac{\sqrt2}{\beta} \Leftrightarrow x_1=V_g.t-\frac{\sqrt2}{\beta}\)
\(V_g.t-x_2=\frac{\sqrt2}{\beta} \Leftrightarrow x_2=V_g.t+\frac{\sqrt2}{\beta}\)
\(\Rightarrow\Delta x=x_2-x_1=\frac{2\sqrt2}{\beta}\)
On a trouvé (question 2) que :
\(\Delta k=(k_2-k_1)=\beta \sqrt2\Rightarrow\Delta x . \Delta k=\frac{2\sqrt2}{\beta} . \beta \sqrt2=8\)
En utilisant la définition : \(V_g=\frac{d\omega}{dk}\simeq\frac{\Delta\omega}{\Delta k}\Rightarrow \Delta\omega=V_g\Delta k\)
mais de plus, l'approximation faite (\(k \rightarrow\omega\) : linéaire) donne \(V_0 = V_g\) non pas nécessairement
Or : \(\Delta x=V_0 . \Delta t\Rightarrow\Delta x=V_g . \Delta t\)
\(\Rightarrow V_g=\frac{\Delta x}{\Delta t}=\frac{\Delta\omega}{\Delta k}\) déplacement de l'enveloppe \(\Rightarrow \Delta\omega . \Delta t=\Delta x . \Delta k\)
8-
Reprenons l'expression déjà vue (question 3) : \(\omega(k)=\omega_0+(k-k_0)\left(\frac{d\omega}{dk}\right)_{k_0}+(k-k_0)^2\left(\frac{d^2\omega}{dk^2}\right)_{k_0}\)
\(\Rightarrow \omega(k)=\omega_0+V_gK'+a . K'^2\)
\(\omega(k)=\omega_0+k'(V_g+a . k')\) ce qui revient à remplacer dans l'expression de \(\psi(x,t) V_g\) par \(V_0+a.k'\)
\(\Rightarrow B(t)=A_0\int_{-\infty}^{+\infty}e^{-\frac{k'^2}{2\beta^2}+ik'(V_g+a.k')t-ik'x}dk'\)
en posant : \(k'^2f(t)=\frac{k'^2}{2\beta^2}+iak'^2t\)
\(\Rightarrow B(t)=A_0\int_{-\infty}^{+\infty}e^{-{k'^2f(t)+ik'(V_g.t-x)}}dk'\)
on posera alors \(L=k'\sqrt{f(t)}~\frac{-i(V_g.t-x)}{2\sqrt{f(t)}}\Rightarrow dL=\sqrt f~dk\) et on est ramené au cas précédent :
par substitution : \(\sqrt2 ~\beta\rightarrow \frac{1}{\sqrt{f(t)}}\) suffit \(V_g\rightarrow V_0\)
9-
\(\Rightarrow\) \(B(x,t)=\frac{A_0\sqrt{f\pi}}{\sqrt{f(t)}}e^{-\frac{(V_0t-x)^2}{4f(t)}}\) (obtenu d'après le résultat de la question 5) et \(\psi(x,t)=B(x,t).\cos(\omega_0t-k_0x)\)
L'enveloppe de modulation : ne se propage plus à la vitesse \(y_0=V_0\) et de plus se déforme à cause du facteur : \(f(t)\)