Propagation d'une fonction ayant une bande spectrale en forme de créneau
Partie
Question
Soit \(f(\omega)\) le spectre (sur la base des exponentielles imaginaires) d'une fonction \(F\) non périodique de variable \(t\), défini par :
\(f(\omega)=A\) pour \(\omega\in\left[\frac{\omega_0-\Delta\omega}{2},\frac{\omega_0+\Delta\omega}{2}\right]\) où \(\Delta\omega\) est quelconque
\(f(\omega)=0\) en dehors de cet intervalle.
Déterminer la fonction \(F(t)\) dont \(f(\omega)\) est le spectre, et en déduire (en notation complexe) l'expression \(\psi(z, t)\) de la propagation de la vibration \(F(t)\) dans la direction \(z\) (la position de la source \(F(t)\) sera prise pour origine de la variable \(z\)).
On admettra l'expression du développement (série de Taylor) d'une fonction autour d'une valeur particulière de sa variable, et on l'appliquera à la fonction \(K(\omega)\), à savoir :
\(K(\omega)=K(\omega_0)+(\omega-\omega_0)\left(\frac{dK}{d\omega}\right)_{(\omega=\omega_0)}+...+\frac{(\omega-\omega_0)^n}{n !}(K^{(n)}(\omega))_{(\omega=\omega_0)}+...\)
On posera : \(\delta \omega=\omega-\omega_0, \frac{\delta\omega}{\omega_0}=\varepsilon, K(\omega_0)=K_0\)
Exprimer le développement précédent en fonction de \(\varepsilon\).
En admettant que la bande \(\Delta\omega\) est très étroite (\(\Delta\omega<<\omega_0\)), montrer que ce développement peut être limité au premier ordre, et en donner l'expression.
On posera : \(\left(\frac{dK}{d\omega}\right)_{(\omega=\omega_0)}=\frac{1}{V_0}\)
En utilisant alors le résultat de la question 1-, déterminer \(\psi(z,t)\).
Mettre ce résultat sous la forme : \(\psi(z, t) = A(z, t).\cos (\omega_0t - K_0z)\)
Représenter la partie réelle de \(\psi(z, t)\) et interpréter ce résultat.
Solution détaillée
1-
\(f(\omega)=A\) pour \(\omega\in\left[\omega_0-\frac{\Delta\omega}{2} ; \omega_0+\frac{\Delta\omega}{2}\right]\)
\(f(\omega)=0\) pour \(\omega\notin\left[\omega_0-\frac{\Delta\omega}{2} ; \omega_0+\frac{\Delta\omega}{2}\right]\)
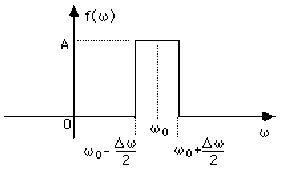
D'une manière générale, pour exprimer la propagation \(\psi(z,t)\) de la fonction \(F(t)\) dont \(f(\omega)\) est le spectre, en notation complexe, il faut :
- exprimer la fonction \(F\) sur la base des fonctions exponentielles [\(f(\omega)\) représente la composante de \(F\) à la valeur \(\omega\)], i.e. :
\(F(t)=\int_{-\infty}^{+\infty}f(\omega).e^{+i\omega t}d\omega\)
exprimer la propagation des fonctions de base \(e^{+i\omega t}\) à la valeur \(\omega\), i.e : \(e^{i(\omega t -K(\omega)z)}\)
d'où l'on déduit qu'une fonction dont la densité d'amplitude vaut \(f(\omega)\) en \(\omega\) se propagera selon l'expression : \(f(\omega)e^{i(\omega t -K(\omega)z)}\)
exprimer la fonction représentant la propagation de \(F\) sur la base des fonctions de base "propagées"
\(\psi(z,t)=\int_{-\infty}^{+\infty}f(\omega)e^{i(\omega t-K(\omega)z)}d\omega\)
Cette expression signifie que la fonction \(F\) représente la source située en \(z=0\), [car : \(\psi(z=0, t) = F(t)\)] , de la vibration qui se propage dans la direction et le sens de l'axe \(z\).
\(F(t)=A\int_{\omega_0-\frac{\Delta\omega}{2}}^{\omega_0+\frac{\Delta\omega}{2}}e^{+i\omega t}d\omega=\frac{A}{it}\left(e^{i(\omega_0+\frac{\Delta\omega}{2})t}-e^{i(\omega_0-\frac{\Delta\omega}{2})t}\right)\)
\(=\frac{2A}{t}e^{+i\omega_0t}\sin\frac{\Delta\omega}{2}t\)
soit : \(F(t)=A\Delta\omega\frac{\sin\frac{\Delta\omega}{2}t}{\frac{\Delta\omega}{2}t}e^{+i\omega_0t}=A\Delta\omega\frac{\sin u}{u}e^{i\omega_0t}\) avec \(u= \frac{\Delta\omega}{2}t\)
Bien que l'on connaisse cette expression de \(F(t)\) il est nécessaire d'exprimer \(F\) sur les fonctions de base (fonctions de \(\omega\)) car, dans le cas général, la propagation n'est pas une simple translation de \(F\), et la vitesse de propagation : \(V(\omega) = \frac{\omega}{K(\omega)}\) est fonction de \(\omega\). Dans le cas particulier où la vitesse (définie par ce rapport) ne dépend pas de \(\omega\), on dit que le milieu est non-dispersif.
Le milieu étant ici dispersif : \(\psi(z,t)=A\int_{\omega_0-\frac{\Delta\omega}{2}}^{\omega_0+\frac{\Delta\omega}{2}}e^{i(\omega t-K(\omega)z)}d\omega\)
2-
\(K(\omega)=K(\omega_0)+\delta\omega\left(\frac{dK}{d\omega}\right)_{(\omega=\omega_0)}+(\delta\omega)^2\left( \frac{d^2K}{d\omega^2}\right)_{(\omega=\omega_0)}+...\)
\(\Rightarrow \frac{K(\omega)}{\omega_0}=\frac{K(\omega_0)}{\omega_0}+\varepsilon\left(\frac{dK}{d\omega}\right)_{(\omega=\omega_0)}+\varepsilon^2\omega_0\left( \frac{d^2K}{d\omega^2}\right)_{(\omega=\omega_0)}+...\)
L'écart \(\delta\omega=\omega-\omega_0\) est au maximum égal à la largeur totale de bande : \(\Delta\omega\)
Si \(\Delta\omega<< \omega_0\), \(\varepsilon\) sera petit devant \(1\), et on aura en négligeant les termes d'ordre supérieur à \(2\) :
\(\frac{k(\omega)}{\omega_0}\approx\frac{K(\omega_0)}{\omega_0}+\varepsilon\left(\frac{dK}{d\omega}\right)_{(\omega=\omega_0)}\Rightarrow k(\omega)\approx K(\omega_0)+\frac{\varepsilon\omega_0}{V_g}=K_0+\frac{\delta\omega}{V_g}\)
en posant : \(K(\omega_0)=K_0\) et \(V_g=\frac{d\omega}{dK}\) vitesse de groupe de l'onde.
3-
Avec cette expression de \(K(\omega)\), la fonction \(\psi(z,t)\) représentant la propagation s'exprime :
\(\psi(z,t)=A . \int_{\omega_0-\frac{\Delta\omega}{2}}^{\omega_0+\frac{\Delta\omega}{2}}e^{i(\omega t-K(\omega)z)}d\omega=\psi(z,t)=A . \int_{\omega_0-\frac{\Delta\omega}{2}}^{\omega_0+\frac{\Delta\omega}{2}}e^{i[(\omega_0+\delta\omega)t-(K_0+\frac{\delta\omega}{V_g})z]}d\omega\)
On pose \(\omega-\omega_0=\delta\omega=\alpha\) comme nouvelle variable d'intégration :
\(\omega\in\left[\omega_0-\frac{\Delta\omega}{2} ; \omega_0+\frac{\Delta\omega}{2}\right]\Rightarrow \alpha\in\left[-\frac{\Delta\omega}{2} ;+\frac{\Delta\omega}{2}\right]\)
\(\psi(z,t)=A . \int_{-\frac{\Delta\omega}{2}}^{+\frac{\Delta\omega}{2}}e^{i[(\omega_0+\alpha)t-(K_0+\frac{\alpha}{V_g})z]}d\alpha=A . e^{i(\omega_0t-K_0z)}\int_{-\frac{\Delta\omega}{2}}^{+\frac{\Delta\omega}{2}}e^{i\alpha(t-\frac{z}{V_g})}d\alpha\)
\(\psi(z,t)=\frac{2A}{t-\frac{z}{V_g}} . e^{i(\omega_0t-K_0z)} . \sin\frac{\Delta\omega}{2}(t-\frac{z}{V_g})=A . \Delta\omega . e^{i(\omega_0t-K_0z)} . \frac{\sin{\frac{\Delta\omega}{2}(t-\frac{z}{V_g})}}{\frac{\Delta\omega}{2}(t-\frac{z}{V_g})}\)

Remarques :
remarques 1 :
Le traitement effectué ici suppose que le milieu est faiblement dispersif, i.e. que les dérivées successives \(\left(\frac{d^nK}{d\omega^n}\right)_{(\omega=\omega_0)}\) ont une faible valeur et que les termes correspondants sont négligeables par rapport au terme contenant la dérivée d'ordre \(1\). Si, de plus, la bande \(\Delta\omega\) est étroite par rapport à \(\omega_0\), la vibration : \(F(t)=A . \Delta\omega . \frac{\sin\frac{\Delta\omega}{2}t}{\frac{\Delta\omega}{2}t} . e^{+i\omega_0t}\) dont on ne considère que la partie réelle :
\(\Re(F(t))=A . \Delta\omega . \frac{\sin\frac{\Delta\omega}{2}t}{\frac{\Delta\omega}{2}t} . \cos(\omega_0t)\) se propage donc selon la partie réelle de \(\psi(z,t)\), soit : \(A . \Delta\omega . \frac{\sin\frac{\Delta\omega}{2}(t-\frac{z}{V_g})}{\frac{\Delta\omega}{2}(t-\frac{z}{V_g})} . \cos(\omega_0t-K_0z)\)
Dans cette expression :
le facteur en \(\frac{\sin u}{u}\) représentant l'enveloppe, est une fonction de (\(t-\frac{z}{V_g}\)) : l'enveloppe se propage donc à la vitesse \(V_g\) (vitesse de groupe).
le facteur \(\cos[\omega_0t-K_0z]\) de pulsation \(\omega_0\) (pulsation moyenne de l'intervalle \(\Delta\omega\)) représentant les oscillations à l'intérieur de l'enveloppe, se propage à la vitesse \(V_0=\frac{\omega_0}{K_0}\) (vitesse de phase).
remarque 2 :
Si la dispersivité est plus grande, on montre en faisant intervenir les termes d'ordre supérieur du développement de \(K(\omega)\), que la propagation de l'enveloppe n'est plus une simple translation : sa forme peut se modifier pendant la propagation (étalement du paquet d'onde).
remarque 3 :
Si le milieu n'est pas du tout dispersif, les vitesses : \(V_g=\frac{d\omega}{dK}\) et \(V_0=\frac{\omega}{K}\) sont égales. Dans ce cas, l'oscillation et son enveloppe se propagent à la même vitesse, soit :
\(A . \Delta\omega . \frac{\sin\frac{\Delta\omega}{2}(t-\frac{z}{V_0})}{\frac{\Delta\omega}{2}(t-\frac{z}{V_0})} . \cos[\omega_0t-K_0z]\)
remarque 4 :
Au lieu de la fonction \(F\) considérée ici, dont le spectre continu \(f(\omega)\) est compris entre 2 pulsations : \(\omega_1=\omega_0-\frac{\Delta\omega}{2}\) et \(\omega_2=\omega_0+\frac{\Delta\omega}{2}\), si on considère la fonction somme de 2 cosinus de pulsations différentes, respectivement \(\omega_1\) et \(\omega_2\).
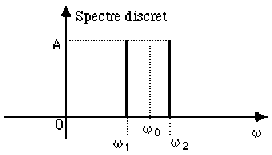
\(\omega_0=\frac{\omega_2+\omega_1}{2}\) et \(K_0=\frac{K_2+K_1}{2}\)
vitesse de la pulsation moyenne \(=V_0=\frac{\omega_0}{K_0}\)
vitesse de l'enveloppe\(=V_g=\frac{\frac{\omega_2-\omega_1}{2}}{\frac{K_2-K_1}{2}}=\frac{\Delta\omega}{\Delta K}\)
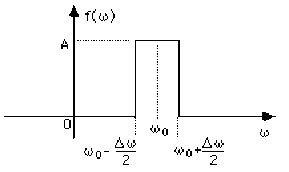
pulsation moyenne du spectre\(= \omega_0\)
vitesse de la pulsation moyenne\(=V_0=\frac{\omega_0}{K_0}\)
vitesse du groupe\(=V_g=\left(\frac{d\omega}{dK}\right)_{\omega=\omega_0}\) autour de la valeur centrale \(\omega_0\)