Fonction cos. réduite à un support borné: élargissement de raies spectrales
Partie
Question
Soit la fonction \(\psi\) définie par :
\(\psi(t)=A\cos\omega_0t\) pout \(t \in[-\frac{\Delta t}{2},+\frac{\Delta t}{2}]\), où \(\Delta t\) est quelconque
\(\psi(t)=0\) en dehors de cet intervalle.
Représenter cette fonction.
Déterminer son spectre \(f(\omega)\), défini par la transformée de Fourier de la fonction \(\psi\).
Montrer que ce spectre est constitué de \(2\) parties (que l'on notera \(f_1(\omega)\) et \(f_2(\omega)\)), telles que \(f_1(-\omega) = f_2(\omega)\) (i.e. symétriques par rapport à \(O\)) et présentant un maximum respectivement en \(- \omega_0\) et \(+\omega_0\).
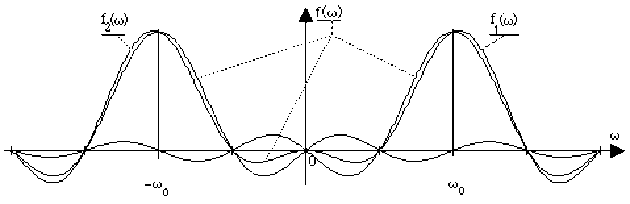
Tracer ce spectre \(f(\omega)\) et le comparer à celui de la fonction périodique : \(\cos\omega_0t\).
On suppose que la durée \(\Delta t\) de cette vibration \(\psi(t)\) est égale à \(10\) fois la période \(T_0\) de la vibration.
Montrer que dans ces conditions, la partie \(f_1(\omega)\) du spectre représente dans la région \(\omega>0\) une contribution au spectre inférieure au \(\frac{1}{30}\) de son amplitude maximum.
On conviendra par suite de négliger la contribution de ce terme dans cette région.
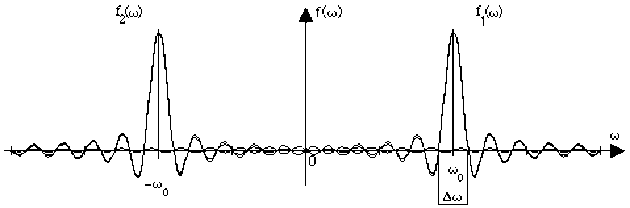
On appellera \(\Delta\omega\) la largeur de la bande spectrale comprise entre les valeurs de \(\omega\) correspondant aux premiers minimums de \(|f(\omega)|\) situés de part et d'autre de \(\omega_0\).
Montrer que le fait de limiter la durée de la vibration \(\psi(t)\) à un intervalle de temps \(\Delta t\) est responsable d'un élargissement de la raie centrale en \(\omega=\omega_0\).
Pour ce faire, on établira la relation : \(\Delta\omega.\Delta t = 4\pi\) .
Solution détaillée
1-
Soit la fonction \(\psi\) définie par :
\(\psi(t)=A\cos\omega_0 t\)
pour \(t\in[-\frac{\Delta t}{2},+\frac{\Delta t}{2}]\) où \(\Delta t\) est quelconque.
\(\psi(t)=0\)
en dehors de cet intervalle
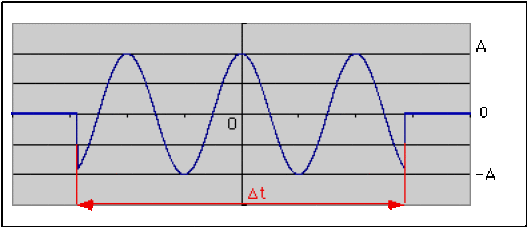
La fonction \(\psi\) est une fonction à support borné, i.e. elle est nulle partout sauf sur l'intervalle \([-\frac{\Delta t}{2},+\frac{\Delta t}{2}]\).
Sur son support, cette fonction est continue et bornée. Sa Transformée de Fourier existe donc, et nous allons la déterminer.
Soit : \(f(\omega)=\frac{1}{2\pi} . \int_{-\infty}^{+\infty}\cos\omega_0 t . e^{-i\omega t} . dt=\frac{1}{2\pi} . \int_{-\frac{\Delta t}{2}}^{+\frac{\Delta t}{2}}\cos\omega_0t . e^{-i\omega t} . dt\)
En utilisant les formules d'Euler, puis en intégrant :
\(f(\omega)=\frac{1}{4\pi}\int_{-\frac{\Delta t}{2}}^{+\frac{\Delta t}{2}}(e^{i\omega_0t}+e^{-i\omega_0t}).e^{-i\omega t}.dt=\frac{1}{4\pi}\int_{-\frac{\Delta t}{2}}^{+\frac{\Delta t}{2}}(e^{i(\omega_0-\omega)t}+e^{-i(\omega_0+\omega)t}).dt\)
\(=\frac{1}{4\pi}\big[\frac{1}{i(\omega_0-\omega)}[e^{i(\omega_0-\omega)t}]_{-\frac{\Delta t}{2}}^{\frac{+\Delta t}{2}}+\frac{1}{-i(\omega_0+\omega)}[e^{-i(\omega_0+\omega)t}]_{-\frac{\Delta t}{2}}^{\frac{+\Delta t}{2}} \big]\)
\(=\frac{1}{4\pi}[\frac{2}{(\omega_0-\omega)}\sin(\omega_0-\omega)\frac{\Delta t}{2}+\frac{2}{(\omega_0+\omega)}\sin(\omega_0+\omega)\frac{\Delta t}{2}]\)
\(=\frac{\Delta t}{4\pi}\left[\frac{\sin(\omega_0-\omega)\frac{\Delta t}{2}}{(\omega_0-\omega)\frac{\Delta t}{2}}+\frac{\sin(\omega_0+\omega)\frac{\Delta t}{2}}{(\omega_0+\omega)\frac{\Delta t}{2}}\right]=f_1(\omega)+f_2(\omega)\)
en posant \(f_1(\omega)=\frac{\Delta t}{4\pi}\frac{\sin(\omega_0-\omega)\frac{\Delta t}{2}}{(\omega_0-\omega)\frac{\Delta t}{2}}\) et \(f_2(\omega)=\frac{\Delta t}{4\pi}\frac{\sin(\omega_0+\omega)\frac{\Delta t}{2}}{(\omega_0+\omega)\frac{\Delta t}{2}}\)
On remarque que : \(f_2(\omega)\) s'obtient à partir de \(f_1(\omega)\) en remplaçant \(\omega\) par \(-\omega\), i.e. : \(f_2(\omega) = f_1(-\omega)\).
le spectre \(f_1(\omega)\) présente un maximum en \(\omega=\omega_0\)
le spectre \(f_2(\omega)\) présente un maximum en \(\omega=-\omega_0\)
En exprimant la fonction périodique \(\cos\omega_0t\) , pour \(t \in [-\infty ; +\infty]\) par la formule d'Euler :
\(\cos\omega_0t = \frac{1}{2} \exp (i\omega_0t) + \frac{1}{2}\exp (-i\omega_0t)\)
on voit donc que le spectre de cette fonction sur la base des exponentielles admet justement pour fréquences \(+\omega_0\) et \(-\omega_0\).
Mais dans le cas d'une fonction périodique le spectre est discret, au lieu que le spectre soit continu dans le cas de la fonction à support borné (voir schémas suivants).
2-
Le schéma (2) correspond à une fonction \(\psi\) dont le support est \(\Delta t = 10.T_0\).
Soit dans ce cas : \(\omega_1\) la valeur de la pulsation correspondant au 1° maximum de la fonction \(f_2(\omega)\) dans la région \(\omega>0\). Ce qui signifie donc que \((\omega_0+ \omega_1)\frac{\Delta t}{2}\) est égal à \(\frac{\pi}{2}\) modulo \(2\pi\).
D'où : \((\omega_0+\omega_1)\frac{\Delta t}{2}=\omega_0.5.T_0+\omega_1.5.T_0=10\pi+\textrm{0,5}\pi\). On a donc :
\(f_2(\omega_1)=\frac{\Delta t}{4\pi}\frac{\sin(\omega_0+\omega_1)\frac{\Delta t}{2}}{(\omega_0+\omega_1)\frac{\Delta t}{2}}=\frac{\Delta t}{4\pi}\frac{\sin\textrm{10,5}\pi}{\textrm{10,5}\pi}=\frac{\Delta t}{4\pi}\frac{1}{30}\) et \(f_1(\omega_0)=\frac{\Delta t}{4\pi}\)
L'amplitude du 1° max de \(f_2(\omega)\) dans la région \(\omega>0\) est donc de l'ordre du \(1/30\) de la valeur du maximum \(f_1(\omega_0)\) de \(f_1\) dans la région \(\omega>0\). [Remarque : \(\sin(u)/u =1\) pour \(u=0\)]
Durée de la fonction \(\psi(t)\) : \(\Delta t=\frac{4\pi}{\omega_0}=2T_0\)
Durée de la fonction \(\psi(t) : \Delta t=\frac{20\pi}{\omega_0}=10T_0\)
Durée de la fonction \(\psi(t)\) : \(\Delta t=\frac{100\pi}{\omega_0}=50T_0\)
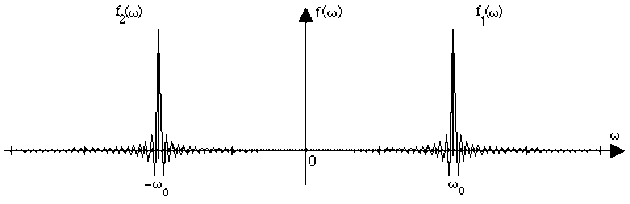
Le spectre \(f(\omega)\) de la fonction \(\psi\) est la somme de \(2\) termes \(f_1(\omega)\) et \(f_2(\omega)\).
Les schémas ci-dessus montrent l'effet de la durée \(\Delta t\) de la fonction \(\psi\) sur la forme de son spectre : le spectre est d'autant plus resserré que la fonction dure plus longtemps. Dans le cas limite de la fonction périodique (durée de \(-\infty\) à \(+\infty\)), le spectre est réduit aux seules valeurs \(- \omega_0\) et \(+ \omega_0\).
3-
La "largeur" du spectre autour de \(\omega_0\) est représentée par la bande centrale \(\Delta\omega = \Omega_2 -\Omega_1\) dont les limites \(\Omega_1\) et \(\Omega_2\) correspondent aux 1° valeurs nulles du sinus, de part et d'autre du maximum (en \(\omega_0\)). (voir schéma précédent). Ces valeurs nulles du sinus correspondent à des arguments multiples de \(\pi\). Entre les limites \(\Omega_1\) et \(\Omega_2\) de la bande, la différence des arguments est donc \(2\pi\).
Considérons la partie \(f_1\) du spectre : \(f_1(\omega)=\frac{\Delta t}{4\pi}\frac{\sin(\omega_0-\omega)\frac{\Delta t}{2}}{(\omega_0-\omega)\frac{\Delta t}{2}}=\frac{\Delta t}{4\pi}\frac{\sin u}{u}\)
\(u=0 \Rightarrow \sin u=0\Rightarrow\frac{\sin u}{u}=1\) correspond au maximum \(f_1(\omega_0) \textrm{ en }\omega = \omega_0\)
\(u_1 = -\pi \Rightarrow \sin u_1 = 0\Rightarrow \frac{\sin u_1}{u_1}=0\) correspond à la valeur \(\omega = \Omega_1\)
\(u_2 = +\pi \Rightarrow \sin u_2 = 0 \Rightarrow \frac{\sin u_2}{u_2} = 0\) correspond à la valeur \(\omega = \Omega_2\)
Les valeurs aux limites de l'intervalle considéré sont en effet :
\(f_1(\Omega_1)=\frac{\Delta t}{4\pi}\frac{\sin(\omega_0-\Omega_1)\frac{\Delta t}{2}}{(\omega_0-\Omega_1)\frac{\Delta t}{2}}=0\) et \(f_1(\Omega_2)=\frac{\Delta t}{4\pi}\frac{\sin(\omega_0-\Omega_2)\frac{\Delta t}{2}}{(\omega_0-\Omega_2)\frac{\Delta t}{2}}=0\)
\(\Rightarrow u_2 - u_1 = (\omega_0- \Omega_2 )\frac{\Delta t}{2} - (\omega_0- \Omega_1). \frac{\Delta t}{2}= 2.\pi\)
\(\Rightarrow(\Omega_1 - \Omega_2).\frac{\Delta t}{2} = 2.\pi\Rightarrow \Delta\omega.\Delta t = 4\pi\)
Cette relation entre la durée \(\Delta t\) de la fonction et l'extension \(\Delta\omega\) du spectre de cette fonction est plus générale que la cadre de cette démonstration. Cette relation est illustrée par les \(3\) schémas précédents.
Elle montre que l'on ne peut pas simultanément réduire autant que l'on veut la durée \(\Delta t\) d'un signal et la largeur \(\Delta\omega\) de son spectre de pulsations temporelles.
Cette limitation n'est pas une question technique (pas seulement), mais elle est plus profondément liée à la nature des "objets théoriques" en jeu dans le modèle ondulatoire.
De la même façon, on peut montrer une relation analogue : \(\Delta K.\Delta z = 4\pi\) qui montre que l'on ne peut pas réduire autant que l'on veut la largeur \(\Delta z\) d'un "objet" et la largeur de la bande spectrale \(\Delta K\) qui représente cet objet.