Série et Transformée de Fourier
Partie
Question
Soit la fonction\( \psi\) définie \(\forall t\in[-\infty,+\infty]\) par :
\(\psi (t) = A (\cos \omega_1t + \cos \omega_2t )\) pour \(t\in[-\frac{\Delta t}{2},+\frac{\Delta t}{2}]\)
\(\psi (t) = 0\) \(\forall t\) en dehors de cet intervalle, où \(\Delta t =\frac{2\pi}{\omega_2-\omega_1}\)
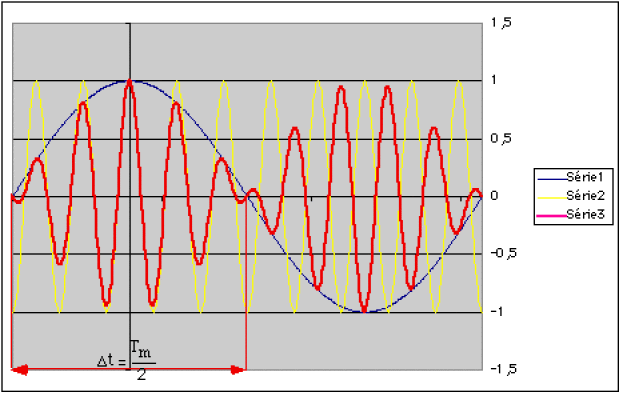
Représenter cette fonction.
Déterminer son spectre\( f(\omega)\).
Comparer \(f(\omega)\) au spectre de la fonction périodique : \(\cos \omega_1t + \cos \omega_2t\).
Application numérique : \(\omega_1 = \frac{9}{11} . \omega_2\).
Rappel de cours
Voir la page Passages à la limite
Solution détaillée
Fonction \(\psi\) du type : \(\left\{\begin{array}{l}\psi(t)=\cos\omega_1t+\cos\omega_2t\textrm{ sur l'intervalle }\Delta t \\ \psi(t)=0 \textrm{ partout ailleurs} \end{array}\right.\)
On transforme la somme en produit : \(\psi(t)=A(\cos(\omega_1t)+\cos(\omega_2t))=2A\underbrace{\cos(\frac{\omega_2+\omega_1}{2}t)}_{\omega_M}.\underbrace{\cos(\frac{\omega_2-\omega_1}{2}t)}_{\omega_m}\)
\(\cos\omega_1t+\cos\omega_2t\equiv2\cos\omega_mt.\cos\omega_Mt\) avec \(\cos\omega_mt\Rightarrow\) facteur de modulation (Série 1) et \(\cos\omega_Mt\Rightarrow\) oscillation moyenne (Série 2)