Spectre discret. Spectre continu.
Partie
Question
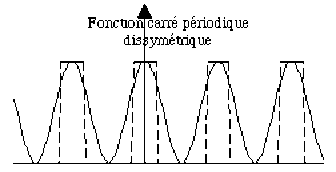
On désigne par \(F\) une fonction créneau de variable \(t\), \(t\in [-\infty,+\infty]\), périodique et de période \(T\).
Chaque créneau, de valeur \(a\) \((a > 0)\) pendant un intervalle de temps \(t_1\) , est séparé du créneau suivant par un intervalle de temps \(t_2\) pendant lequel la fonction est nulle. La période \(T\) de la fonction \(F\) est ainsi \(T = t_1 + t_2\) .
Montrer qu'il est possible de choisir l'origine des temps de sorte que la fonction \(F\) ainsi définie ait un développement en Série de Fourier de forme particulière :
\(F(t)=A_0+\displaystyle{\sum_{n=1}^{n=\infty}}A_n\cos n\omega_1t\) où \(\omega_1=2\pi\nu_1=\frac{2\pi}{T}\)
Montrer que \(A_0=\frac{at_1}{T}\)
Montrer que \(A_n=\frac{2a}{n\pi} . \sin\frac{2\pi t_1}{T}\)
Dans le cas particuliers suivants : \(\frac{t_1}{T}=\frac{1}{2} \textrm{ et }\frac{t_1}{T}=\frac{1}{8}\) donner le développement en série de Fourier de ces fonctions \(F\) et représenter leur spectre : \(\{n,\frac{A_n}{A_1}\}\).
Dans le cas particulier où \(t_1<T\) on notera \(f_n\) la fonction définie sur l'ensemble discret des valeurs \(\omega_n\) de \(\omega\), et telle que : \(f_n(\omega_n)=\frac{A_n}{\omega_1}\)
Exprimer \(f_n(\omega_n)\).
Montrer que, lorsque \(T\rightarrow \infty\) : la fonction \(f_n\) tend vers une fonction \(f\) défini sur l'ensemble continu des valeurs de \(\omega\), et telle que :
\(\displaystyle{\lim_{T\rightarrow\infty}f_n(\omega_n)=f(\omega)=\frac{a . t_1}{\pi}\frac{\sin(u)}{u}}\), où l'on explicitera \(u\) en fonction de \(\omega\).
Déterminer (sur la base des exponentielles complexes) le spectre [noté ici \(g(\omega)\)] d'une fonction \(\psi\) non périodique valant \(a\) pendant un intervalle de temps \(t_1\) centré sur l'origine, et nulle ailleurs.
Comparer \(|g(\omega)|\) à l'expression du spectre \(f(\omega)\) trouvé à la question précédente et commenter.
Tracer le graphe : {\(\omega,g(\omega)\)}.
Rappel de cours
Voir la page Passages à la limite
Solution détaillée
1-
Le développement de la fonction \(F\) est pair
\(\Rightarrow\) la fonction \(F\) est paire
2-
\(A_0=\frac{1}{T_1}\int_{(T_1)}F(t)dt=\frac{a.t_1}{T}\)
3-
\(A_n=\frac{2}{T_1}\int_{(T_1)}F(t)\cos(n\omega_1t)dt=\int_{-t_{1/2}}^{+t_{1/2}}\cos(n\omega_1t)dt=\frac{2a}{T_1}\frac{2a}{T_1}\left[\frac{\sin n\omega_1t}{n\omega_1}\right]_{-t_{1/2}}^{+t_{1/2}}\)
\(A_n=\frac{2a}{T_1}\frac{1}{n\omega_1}\left[\sin(n\omega_1\frac{t_1}{2})-\sin(n\omega_1(-\frac{t_1}{2}))\right]=\frac{4a}{T_1n\omega_1}\sin(n\omega_1\frac{t_1}{2})\)
\(\omega_1T_1=2 \pi \Rightarrow n\omega_1\frac{t_1}{2}=\frac{n\omega_1T_1t_1}{T_12}=n\pi\frac{t_1}{T}\) et \(\frac{4a}{n\omega_1T_1}=\frac{2n}{n\pi}\)
\(\Rightarrow A_n=\frac{2a}{n\pi}\sin n\pi\frac{t_1}{T}\)
En posant \(u_n=n\pi\frac{t_1}{T}\Rightarrow A_n=\frac{2a}{n\pi}n . \pi . \frac{t_1}{T} . \frac{\sin u_n}{u_n}=\frac{2at_1}{T} . \frac{\sin u_n}{u_n}\)
Le coefficient \(\frac{2at_1}{T}\) ne dépend pas de \(n\Rightarrow A_n\) est proportionnel à \(\frac{\sin u_n}{u_n}\)
4-
\(A_n=2a\frac{t_1}{T}\frac{\sin n\pi\frac{t_1}{T}}{n\pi\frac{t_1}{T}}\)
\(\frac{t_1}{T}=\frac{1}{2}\Rightarrow A_n=a\frac{\sin\frac{n \pi}{2}}{\frac{n \pi}{2}}=\frac{2a}{n\pi}\sin n\frac{\pi}{2}\Rightarrow\) tous les termes pairs ont une amplitude nulle.
\(n\) impair \(\Rightarrow\) on pose \(n =2m+1 \Rightarrow A_{2m+1}=\frac{2a(-1)^m}{(2m+1)\pi}\)
\(\frac{t_1}{T}=\frac{1}{8}\Rightarrow A_n=\frac{a}{4}\frac{\sin\frac{n \pi}{8}}{\frac{n \pi}{8}}\Rightarrow\) tous les termes de rang \(n\) multiple de \(8\) ont une amplitude nulle.
\(A_1=\frac{a}{4}\frac{\sin\frac{\pi}{8}}{\frac{\pi}{8}}\)
Calcul :
\(\sin \frac{x}{2}=\sqrt{\frac{1-\cos x}{2}}\)
\(\sin \frac{\pi}{8} = \sqrt{\frac{1-\sqrt{\frac{2}{2}}} {2}} = \frac{1}{2} \simeq \mathrm{0,38268...}\)
\(\frac{A_n}{A_1}=\frac{\sin\frac{n\pi}{8}}{\frac{n\pi}{8}}\frac{\frac{\pi}{8}}{\sin\frac{\pi}{8}} \Rightarrow \frac{A_n}{A_1}\simeq(\textrm{1,026})\frac{\sin\frac{n\pi}{8}}{\frac{n\pi}{8}}\)
5-
\(f_n(\omega_n)=\frac{A_n}{\omega_1}=\frac{2at_1A_n}{\omega_1T}\frac{\sin u_n}{u_n}\) avec \(u_n=n\pi\frac{t_1}{T}=\frac{n \pi\omega_1t_1}{\omega_1T} \textrm{ avec }\omega_1T=2\pi\)
et \(n\omega_1=\omega_n\Rightarrow u_n=\omega_n\frac{t_1}{2}\)
\(f_n(\omega_n)=a\frac{t_1}{\pi}\frac{\sin u_n}{u_n}\)
\(\omega_1\rightarrow0\Rightarrow \omega_n=2\omega_1 \rightarrow\) variable continue \(\omega\)
\(u_n\rightarrow u\)
\(f_n(\omega_n)\rightarrow f(\omega)=\frac{at_1}{\pi}\frac{\sin u}{u}\) avec \(u=\omega\frac{t_1}{2}\)
ou \(f(\omega)=\frac{2a}{\pi\omega}\sin(\omega\frac{t_1}{2})\)
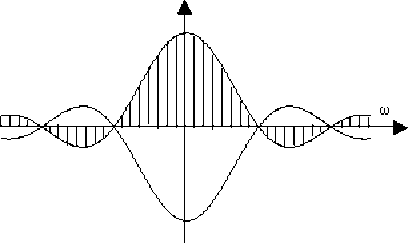
Schéma ci-dessus: enveloppe \(f(\omega)\) et spectre d'une fonction périodique carré dissymétrique, pour \(t_1 = T/8\), (l'harmonique de rang \(8\) a une amplitude nulle).
6-
\(g(\omega)=\frac{1}{2\pi}\int_{-\infty}^{+\infty}F(t)e^{-i\omega t}dt\)
\(\Rightarrow g(\omega)=\frac{1}{2\pi}a\int_{-t_1/2}^{+t_1/2}e^{-i\omega t}dt=\frac{a}{2\pi}\left[\frac{e^{-i\omega t}}{-i\omega}\right]_{-t_1/2}^{+t_1/2}\)
\(=\frac{a}{\pi\omega}(\frac{1}{-2i})[e^{-i\omega t_1/2}-e^{+i\omega t_1/2}]=\frac{a}{\pi\omega}\sin(\omega\frac{t_1}{2})=g(\omega)\)
\(\omega \in[-\infty, +\infty]\)
En utilisant le résultat de la question précédente, on trouve donc \(g(\omega) = \frac{1}{2}f(\omega)\)
6-a- Commentaire
On vérifie que \(g(\omega)\) est la limite de \(\frac{C_n}{\omega_1}\) quand \(\omega_1\) tend vers \(0\) (alors que \(f(\omega)=\lim\frac{A_n}{\omega_1})\)
\(C_n=\frac{1}{T}\int_{(T_1)}F(t)e^{-in\omega_1t}dt\) (avec \(F_n=\displaystyle{\sum_{n=-\infty}^{n=+\infty}C_ne^{in\omega_1t}}\))
\(=\frac{1}{T}a\int_{-t_1/2}^{+t_1/2}e^{-in\omega_1t}dt=\frac{a}{T}\left[\frac{e^{-in\omega_1t}}{-in\omega_1}\right]_{-t_1/2}^{+t_1/2}\)
\(=\frac{2a}{n\omega_1T}\frac{-e^{-in\omega_1t_1/2}+e^{+in\omega_1t_1/2}}{+2i}=\frac{2a}{2\pi n}\sin(n \omega_1\frac{t_1}{2})\)
\(\Rightarrow \frac{C_n}{\omega_1}=\frac{a}{\pi\omega_1}\sin(\omega_n \frac{t_1}{2})\rightarrow \frac{2a}{2\pi\omega_n}\sin(\omega_n\frac{t_1}{2})=g(\omega)\) (ce qui était prévu !)
Plus généralement, les termes sont nuls pour : \(\omega_n\frac{t_1}{2}=N\pi\) soit : \(\omega_n=N\frac{2\pi}{t_1}\)
Cas particulier : \(\tau=\frac{1}{8}\) (schéma précédent)
\(\Rightarrow \frac{A_n}{A_1}=\frac{\frac{\pi}{8}}{\sin\frac{\pi}{8}}\frac{\sin\frac{n\pi}{8}}{\frac{n \pi}{8}}\)
\(A_1=\frac{2a}{\pi}\sin\frac{\pi}{8}\simeq\textrm{0,3826...}\)
6-b- Dans le cas d'une fonction réelle
à partir du développement en exponentielles on peut retrouver un développement en cosinus.
\(F(t)=\int_{-\infty}^{+\infty}g(\omega)e^{i\omega t}d\omega ~\) \(g(\omega)\) est paire
\(=\int_{-\infty}^{+0}g(\omega)e^{i\omega t}d\omega+\int_{-0}^{+\infty}g(\omega)e^{i\omega t}d\omega\)
Changement de variable \(\Omega=-\omega\) pour que \(\Omega\) soit \(>0\)
\(\Rightarrow F(t)=\int_{\Omega=+\infty}^{\Omega=0}g(\Omega)e^{i\Omega t}(-d\Omega)+\int_{\omega=0}^{\omega=\infty}g(\omega)e^{i\omega t}d\omega\)
\(g(\Omega)=g(\omega)\) car \(g\) est paire \(\Rightarrow F(t)=\int_0^{\infty}g(\omega) e^{ - i\omega t}d \omega~ \int_{0}^{+\infty} g(\omega) e^{i \omega t} d \omega\)
\(\Rightarrow F(t)=\int_0^{\infty}g(\omega)(e^{i\omega t}+e^{-i\omega t})d\omega=2\int_0^{\infty}g(\omega)\cos\omega t ~d\omega\)
\(F(t)\) est développable en série de \(\cos(\omega_nt)\Rightarrow\) par passage à la limite, on a une transformée de Fourier en \(\cos(\omega t)\)
\(\displaystyle{\lim_{(\omega_1\rightarrow0)} \frac{A_n}{\omega_1}=f(\omega)}\) avec pour spectre \(f(\omega)=2g(\omega)\) qui est bien la relation trouvée.
Remarque : cet exercice permet de montrer le passage à la limite (lorsque la période de la fonction créneau carré tend vers l'infini). On obtient alors un spectre continu qui s'exprime sur la base des \(\cos(\omega t)\).
Notez cependant qu'au delà de cet exercice, l'expression usuelle des transformées de Fourier se fait sur la base des \(\exp(i\omega t)\).