Série de Fourier et périodicité
Partie
Question
1- Montrer que le développement en série de Fourier de la fonction \(F\) :
\(F(t)=A_0+\displaystyle{\sum_{n=1}^{n=\infty}A_n\cos n\omega_1t+B_n\sin n\omega_1t}\)
peut se mettre sous la forme équivalente : \(F(t)=\displaystyle{\sum_{n=0}^{n=\infty}A_n\cos(n\omega_1t+\varphi_n)}\)
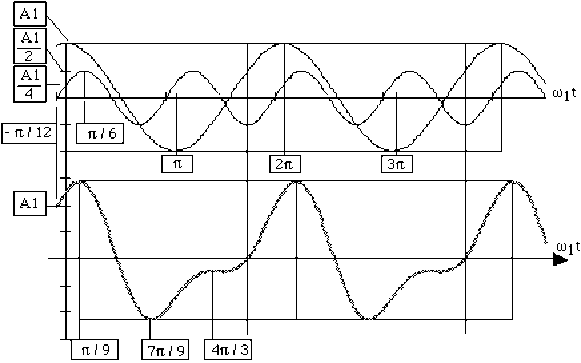
2- Représenter ci-dessous (sur un intervalle de 2 périodes) le graphe de la fonction périodique particulière suivante \(F(t)\) :
\(\omega_1t\rightarrow G(\omega_1t)=F(t)=A_1\cos\omega_1t+\frac{A_1}{2}\cos(2\omega_1t-F(\frac{\pi}{3}))\)
Si vous disposez d'un micro-ordinateur, réalisez un programme de calcul pour tracer le graphe de \(G\).
Vérifiez le tableau de variations suivant, puis tracer le graphe de \(G(\omega_1t)\).
\(\omega_1t\) | \(\frac{\pi}{9}\) | \(\frac{7\pi}{9}\) | \(\frac{4\pi}{3}\) | ||||
\(\frac{dF(t)}{dt}\) | + | 0 | - | 0 | + | 0 | + |
\(\frac{F(t)}{A}\) | Maximum 1.41 | Minimum -1.15 | Inflexion -0.25 |
3- La fonction \(F(t)\) est-elle paire ? impaire ?
Commenter ce résultat en se reportant à la question \(c\) de l'exercice précédent.
Le spectre de \(F\) donne-t-il toute l'information sur \(F\) ?
Solution détaillée
1-
\(F(t)=A_0+\displaystyle{\sum_{n=1}^{n=\infty}A_n\cos n\omega_1t+B_n\sin n\omega_1t} \Rightarrow\)On pose \(\left|\begin{array}{c} A_n=a_n\cos\varphi_n \\ B_n=a_n\sin\varphi_n \end{array} \right|\)
\(\Rightarrow\tan\varphi_n=\frac{B_n}{A_n}\) permet d'exprimer \(F(t)\) sous la forme :
\(F(t)= A_0+\displaystyle{\sum_{n=1}^{\infty}a_n[\cos\varphi_n\cos n\omega_1t-\sin\varphi_n\sin n\omega_1t]}\)
\(=A_0+\displaystyle{\sum_{n=0}^{n=\infty}a_n\cos(n\omega_1t-\varphi_n)}\)
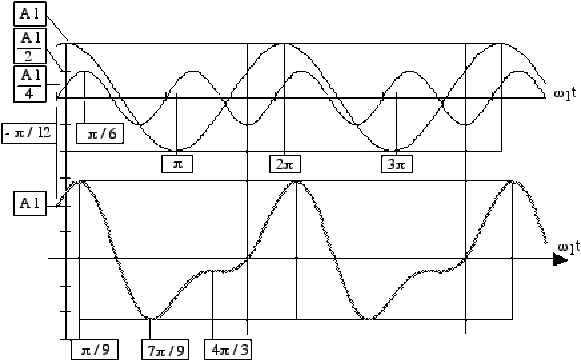
2-
Graphe de la fonction : \(\omega_1t\rightarrow A_1\cos\omega_1t+\frac{A_1}{2}\cos(2\omega_1t-\frac{\pi}{3})\)
3-
\(F\) n'est ni paire ni impaire \(\Rightarrow\) doit s'exprimer comme combinaison linéaire de fonctions paire et impaire.
On peut par exemple poser : \(\cos(2\omega_1t-\frac{\pi}{3})=\cos2\omega_1t . \cos\frac{\pi}{3}+\sin2\omega_1t . \sin\frac{\pi}{3}\)
\(\cos\frac{\pi}{3}=\frac{1}{2} \quad \sin\frac{\pi}{3}=\frac{\sqrt3}{2}\Rightarrow \cos(2\omega_1t-\frac{\pi}{3})=\frac{1}{2}\cos2\omega_1t+\frac{\sqrt3}{2}\sin2\omega_1t\)
\(\Rightarrow F(t)=\underbrace{A_1\cos\omega_1t+\frac{A}{4}\cos2\omega_1t}_{(paire)}+\underbrace{\frac{\sqrt3}{4}A_1\sin2\omega_1t}_{(impaire)}\)
\(\Rightarrow\) Le spectre sous la forme \(\{ \omega_n, A_n, \varphi_n \}=[(\omega_1, A_1, 0) ;(2\omega_1 ; \frac{A_1}{2} ; -\frac{\pi}{3})]\) ou sous la forme \(\{ \omega_n, A_n, B_n \}=[(\omega_1, A_1, 0) ;(2\omega_1, \frac{A_1}{4}, \frac{\sqrt3}{2}A_1]\) donne une représentation équivalente à l'expression de la fonction \(F\).